List of compression Member Posts-part 3.

Last Updated on March 7, 2026 by Maged kamel

A summary is created for the last seven posts on compression members, including images and brief descriptions for each post.

List of compression Member Posts-part 3.

Solved problem 4-16 using the French equation.

This is the 1st post of the Compression Member Posts-part 3, which includes a solved problem 4-16 from Prof. Alan Williams’s book, Structural Engineering Reference Manual.

A sway frame with two spans is given, for which the effective length factor K is required for the given members. The French equation was made for side sway Uninhibited- unbraced frame, for the k value, which is =sqrt(1.6*GA*Gb+4(Ga+Gb)+7.5)/ sqrt of(GA+Gb+7.5).

A calculation for k is performed and compared with the k value from the side sway uninhibited diagrams previously included in post 20. Solved problem 4-16 for k factor.

This is the list of post 21: Solved problem 4-16 using the French equation.

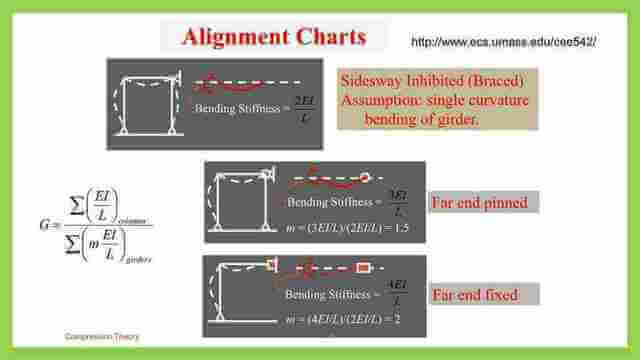
Modification to the Alignment Chart Braced Frame.

This is the 2nd post in the Compression Member Posts, Part 3 series, which covers how to consider column adjustments for different end conditions and how to determine the m value for end conditions of girders in braced frames.

This is the list of post 22: Modification to Alignment Chart Braced Frame.

Solved problem 7-2 for frames-Two parts a,b.

This is the 3rd post of the compression Member Posts-part 3, which includes Example 7.2 from Prof. McCormack’s book. Determine the k values for the columns shown in the given frame in Fig. 7.6.

Here, W sections have been tentatively selected for each frame member, and their I/L values are determined and shown in the figure.

This is the list of post 23: Solved problem 7-2 for k for frame 1/3.

This is the list of post-23a: Solved problem 7-2 for frames

Solved problem 7-2 for frames-part 3.

This is the 4th post of the compression Member Posts-part 3, which includes starting by joint H, and joint H at joint H, no upper column, G=sum(EI/L), which is=20.47/ sum(EI/L) for girder Gh =26.67, Gh=(20.47/26.67)=0.675.

For Gg at joint G, we have two columns: GH, GF, and Gc = (20.47 + 31.67) / sum of (mEI/L) for girders CG and GJ. The m value is 1 at GC and 1.5 for girder GJ, due to the hinge at the far joint. The denominator is (1*70 + 1.5*21.25). Gg = 0.5118.

This is the list of post-24: Solved problem 7-2 for frames-part 3.

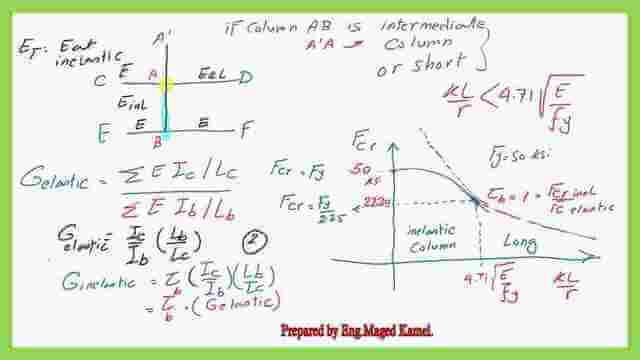
Stiffness reduction factor for inelastic columns.

This is the 5th post of the compression Member Posts-part 3, which covers the difference between the modulus of elasticity E and the tangent modulus of elasticity Et, and under what conditions we use Et?

The second point, τb, or the stress-reduction factor, applies to short or medium columns.

This is the list of post-25: Stiffness reduction factor for inelastic columns. I have added another post, which is post 25A.

Post 25a-Stiffness reduction factor for inelastic columns-part 2, in which I have, through calculations, derived the values of τb in Table 4-13.

Solved problem 4-13 for the stiffness reduction factor.

This is the 7th post of the Compression Member Posts-part 3, which includes Example 4.13, from Prof. Alan Williams’s book. A W10 ×54 of A992 steel is used as a column. It is subjected to a service dead load of 100 kips and a service live load of 200 kips.

If the slenderness ratio makes this member an inelastic column, what is the stiffness reduction factor, tb?

This is the list of post-26: Solved problem 4-13 for the stiffness reduction factor.

Solved problem 4-14 for the effective length factor.

This is the 8th post in the Compression Member Posts-part 3 series, which includes Example 4.14 from Prof. Alan Williams’s book. A rigid unbraced frame is shown in Figure 4.17. All members are oriented so that bending is about the strong axis.

Lateral support is provided at each joint by simply connecting bracing perpendicular to the frame. Determine the effective length factors for member AB with respect to each axis. The service dead load is 35.5 kips, and the service live load is 142 kips. A992 steel is used.

This is the list of post-27: Solved problem 4-14, part 1, for the effective length factor.

This is the second link to post 28: Solved problem 4-14 part 2 for the effective length factor.

Here is the list of compression members in part-2.

Here is the List of compression member posts in part-1.

For a good A Beginner’s Guide to the Steel Construction Manual, 14^th ed. Chapter 7 – Concentrically Loaded Compression Members.

For a good A Beginner’s Guide to the Steel Construction Manual, 15^th ed. Chapter 7 – Concentrically Loaded Compression Members.

For a good A Beginner’s Guide to the Steel Construction Manual, 16^th ed. Chapter 7 – Concentrically Loaded Compression Members.