List of compression Member Posts-part 2.

Last Updated on March 5, 2026 by Maged kamel

List of compression Member Posts-part 2.

11- Local Buckling stiffened and unstiffened.

This is the first post in the Compression Member Posts-part 2, which includes the local buckling classification of sections. Local buckling sections are classified as non-slender or slender.

For non-slender elements, we have two factors: one for the flange and one for the web. If the b flange / t flange < a certain ratio λr. The section is non-slender. The ratio, which we have already discussed via tables, is also essential. h web/ t web < λr.

For a particular factor, the section is non-slender; if it is bigger than λr shown in the table, then the section is slender, and the coefficient is reduced.

There are two coefficients: Qs and Qa. Qs is for the flange; if λ>, the ratio is given, while Qa is for the effective area/ A gross. Non-slender not exceeding λr, from table B4.1a,

This is the link to post 11: Local Buckling stiffened and unstiffened.

12- Solved problem 5-2 for local buckling.

This is the 2nd post in the Compression Member Posts-part 2, which includes solved problem-5-2, quoted from Prof. Jack McCormac’s handbook. The given W section is W#12×72, a non-slender section.

a) Using the column critical stress values in Table 4-22 of the Manual, determine the LRFD design strength and the ASD allowable strength for the column shown in Fig. 5.8.

If 50-KSI steel is used. (b) Repeat the problem, using Table 4-1 of the Manual. (c) Calculate and, using the equations of AISC Section E3,

This is the link to post 12: Solved problem 5-2 for local buckling.

13- A solved problem 5-3 for local buckling.

This is the 3rd post in the Compression Member Posts-part 2 series, which includes Example 5-3 from Prof. Jack McCormac’s handbook. A square HSS section measuring 18 x 15 x 1/2 inches is used for an 18-ft-long column with simple end supports. The column section is non-slender.

(a) Determine Φc*Pn and Pn/Ωc with the appropriate AISC equations.
(b) Repeat part (a) using Table 4-4 in the AISC Manual. A step-by-step guide is provided.

This link to post 13: A solved problem 5-3 for local buckling.

  14- Solved problem 6-8 for local buckling.

This is the 4rth post of the compression Member Posts-part 2, which includes solved problem-6-8 from Prof. Jack McCormac’s handbook. Determine the axial compressive design strength and the allowable design strength of a 24-ft HSS column section.

The base of the column is considered to be fixed, while the upper end is assumed to be pinned.

This is the link to post 14: Solved problem 6-8 on local buckling.

This is the link to post 14a: Problem-6-8 for local buckling-CM#15 For HSS section.

15- A solved problem 6-19-4 for local buckling.

This is the 6th post of the Compression Member Posts-part 2, which includes a solved problem -16-19-4 from Charles G. Salmon’s handbook. Example 6-19-4 Determine the nominal axial compressive strength φc*Pn for the nonstandard shape of Fig. 6.19.4 for an effective length KL equal to 8 ft. Use Fy = 100 ksi and the AISC LRFD Method.

This is the link to post 15: A solved problem 6-19-4 for local buckling.

16-A solved problem 5-10 for local buckling.

This is the 7th post of the Compression Member Posts-part 2, which includes a new example 5-10 from the unified design of steel structures by   Louis  F. Geshwendener.

In solved problem 5-10. It is required to determine the available strength of a slender-web compression member, with a section W16x26, acting as a column, with lcy = 5.0 ft.

This link to post 16: A solved problem 5-10 for local buckling. Two more posts have been added.

Post 16a- Solved Problem 5-10 with more iterations-Fcr value. This is the same solved problem 5-10 from the Unified Design of Steel Structures by Prof. Louis F. Geshwendener. It is required to determine the available strength of a slender-web compression member. The steel section is W16x26 as a column with a length of 5.0 ft. The solution is based on Cm#14.

Post 6b-Available Strength for slender W section-CM#15. In solved problem 5-10. It is required to determine the available strength of a slender-web compression member, with a section W16x26, acting as a column, with lcy = 5.0 ft. The solution is based on CM#15, AISC-360-16. I have chosen a height of 6 feet to check our estimate with Table 6-2.

17-Alignment chart part 2.

This is the 10th post in the Compression Member Posts-part 2 series, which includes the alignment chart and conditions for anti-symmetrical curvature of the unbraced frame.

The Nomograph was based on the assumption of double curvature. We have a bending moment at one end, but at the other end, there is another moment, equal in magnitude, that will cause anti-symmetrical curvature.

This is the link to post 17: Alignment chart, part 2.

18-A Review of portal frames.

This is the 11th post of the Compression Member Posts-part 2, which includes how to make a structural analysis. We give an example: a frame with two hinged supports is subjected to a force on the left side.

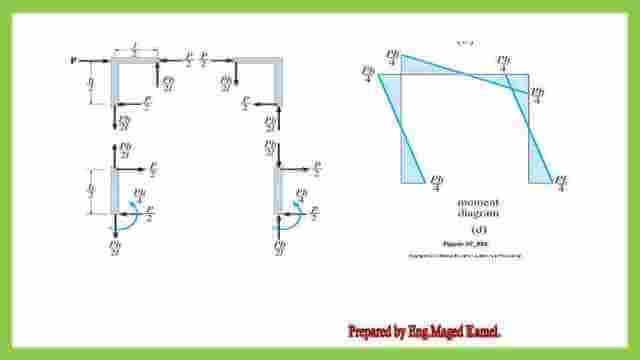
The frame can be analyzed by dividing it into two parts: the first has antisymmetric loading, and the second has symmetric loading. Due to that loading, the elastic curvature.

This is the link to post 18: A Review of Portal Frames.

The second post is Post 18a-Analysis of portal frame-fixed supports at base.

19-Modification to the alignment chart of the unbraced frame.

This is the 13th post in the Compression Member Posts-part 2 series, which discusses adjustments to the G equation because the end condition for the girder does not meet the requirement.

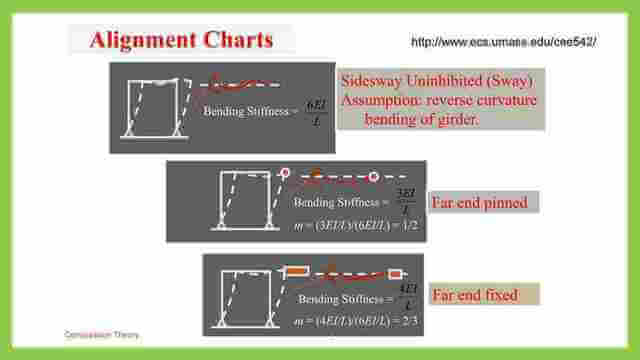
This is the link to post 19: Modification to the alignment chart for the unbraced frame.

20-Solved problem 4-16 for k factor.

This is the 14th post of the Compression Member Posts, Part 2, which includes our example, 4-16, from Prof. Alan Williams’s book, Structural Engineering Reference Manual. A sway frame is an Unbraced or Unstiffened frame. The sway frame shown consists of members with identical I/L values.

Determine the effective length factor for columns. 12 and 34, he has not included any values for the length of girders or the height of columns. We can assume that h and L are the same; we need the K value for the two columns, 12 and 34.

This link to post 20: Solved problem 4-16 for k factor. The verification of the K values by using the French equation is done in post 21 in the list of compression posts, Part 3.

Here is the List of compression member posts in part-1.

The following list of compression member posts is part 3.

For a good A Beginner’s Guide to the Steel Construction Manual, 14^th ed. Chapter 7 – Concentrically Loaded Compression Members.

For a good A Beginner’s Guide to the Steel Construction Manual, 15^th ed. Chapter 7 – Concentrically Loaded Compression Members.

For a good A Beginner’s Guide to the Steel Construction Manual, 16^th ed. Chapter 7 – Concentrically Loaded Compression Members.