Stiffness reduction factor for inelastic columns.
Introduction to the Tangent modulus of elasticity.
This is a new subject, for which, we will talk about the difference between the modulus of elasticity E and the other modulus of elasticity Et, which is the tangent modulus of elasticity, and in what conditions do we use the Et?


The second point, after God’s well, τb, or the stress reduction factor, is for the case of short or medium columns.
In front of you, is the slide, quoted from Prof. Segui’s book, page no.114.In brief. The long columns, the compression stress for these columns, just only reaches the Proportional limit stress, which is a portion of Fy.
He pointed out in the solved example 4-1, that the stress at buckling is Pcr/A, Pcr is the critical load and A is the area.
The value is =19.10 ksi, which is well below the proportion limit for any grade of structural steel. Thus for long columns, the stress on that column will be nearly close to the stress at the proportional limit or smaller.
For the inelastic columns, short or intermediate columns due to the residual stress, which is created due to the change of temperature, heating, and cooling due to the fabrication process, there will be a variation of stresses for the parts of the structural steel column.
Accordingly, there is a change in the relation to the graph between stress and strain, for a column, which can be represented by an inclined line, up to the proportional limit stress followed by a curved graph till the failure occurs.
Introduction to a new value of E which is Et.
Then, the question will be how to estimate the modulus of elasticity for the short or Intermediate column. Prof. Fredric Engesser has proposed several trials, by getting the slope values between the proportional limit point to the failure point and proposed a new tangent modulus of elasticity for Short and Intermediate columns.
The Euler equation Pcr=π^2EI/L^2, for the elastic failure, the expression can be modified to become, after replacing the E expression since by Et, Pcr=π^2Et*I/L^2, since the slope, Et is smaller than E slope at the Euler equation, or the initial modulus of elasticity.


For any material, the critical buckling stress can be plotted as a function of slenderness as shown in Figure 4.6. Later the new studies proved, that we can use his method as follows, for the first part of the graph between L/r and Fcr.
If we extend the slope of the Fcr=π^2*E/(l/r)^2 at the point at which Fcr=Fy/2.25, represents the point at which we differentiate between long and short columns.
As we remember that at the point of Kl/r=4.71*sqrt(E/fy), then there will be another curve, for which, we estimate the proposed critical stress by the Aisc equation.
If we fit the two curves, one for elastic buckling and the other for inelastic buckling, to become tangent to each other. When curves are tangents, then the left side curve represents the inelastic columns and we can write the expression for Fcr= π^2* Et/(l/r)^2.
Now, for the inelastic buckling zone for any value of Kl/r and compare the values estimated by Fcr estimated by the Euler equation, and the value estimated by using the Engesser equation.
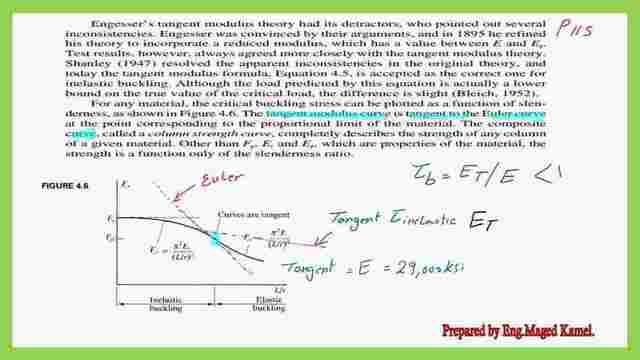

We will find that Fcr inelastic is< Fcr from Euler’s equation, then Fcr inelastic/ Fcr elastic is called τ and is <1.
The modified value of the stiffness ratio at a joint in terms of E and stiffness reduction factor.
How to use this information for the alignment chart for columns?
For instance, if we have a column line A’AB, column AB is inelastic while the intersection beams are elastic. The column has an intersection with two beams, EB and BF, the G value at joint b is represented as Gb=∑EI/L column/=∑EI/L beam. The E for the column will be Et.
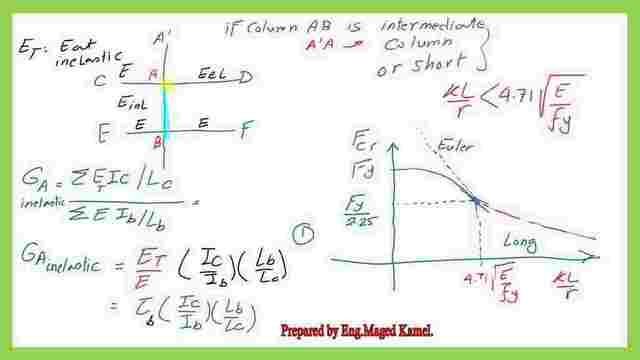

Let Et/E=τb, which is the stiffness reduction factor, the graph between Kl/r and the Fcr as shown, and the tangency point the value of Fcr=fy/2.25, which is closer to the proportional limit value of stress. in the next slide.
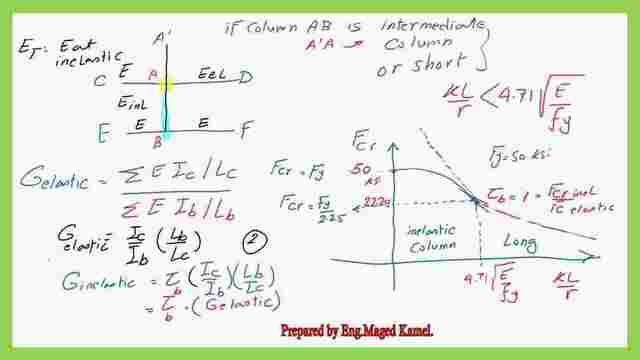

Consider the case of elastic columns and elastic beams, E will cancel each other, then G elastic=(Ic/Ib)*(Lb/Lc), while G inelastic= τb*(Ic/Ib)*(Lb/Lc) = G elastic*τb, τb=Et/E <1.
At P-117, we quote, the column buckling problem can also be formulated in terms of fourth-order differential equations. this proves to be convenient when dealing with a boundary condition other than pinned ends. hence k value can be included in the equation.
Pcr at elastic failure=Pcr=π^2E*A/(k*L)^2, or for inelastic columns, Pcr=π^2Et*A/(k*L)^2, columns given by 4.6b, dividing it by the cross-section area gives the buckling stress


The Fcr value is obtained by dividing Pcr by the area. Fcr inelastic =π^2Et*/(k*L)^2, and G- inelastic=G-elastic*Et/E which is τb.
From Galamblos, Fcr inelastic= (1-λ^2/4)*Fy, the λ^2 =Fy/Fcr, according to the elastic curve.In the next slide, the green graph is the Euler curve, the other graph, which is in a yellow curve is the inelastic column curve and is tangent to the elastic column curve.


This is the pdf file used in the illustration of this post.
A very useful external link is Chapter 7 – Concentrically Loaded Compression Members.
The next post will be a Stiffness reduction factor for inelastic columns-part 2.

