Mohr’s Circle of Inertia part-2.
Point of minimum value of inertia.
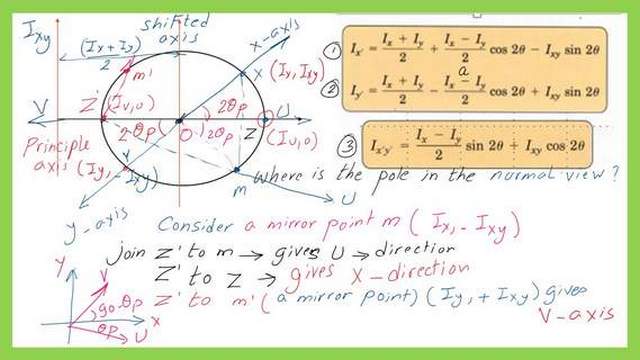
The point of the minimum value of inertia is point Z’ where the Ixy value equals zero. What about the direction of the V axis? The direction is obtained from Mohr’s circle of inertia by an enclosed angle of (180-2θp) in the anti-clockwise or (2θp )from the Y-axis in the clockwise direction.
While in the Normal view, it has an angle of (90-θp) from the x-axis in the anti-clockwise direction.
The expression of tan 2θp.
In Mohr’s Circle of Inertia part-2, the value 2θp can be estimated from the third equation by setting Ix’y’ to be equal to zero, this will give tan 2θp value as equal to (-Ixy/(Ix-Iy/2). The negative sign will include that the angle is in the clockwise direction.
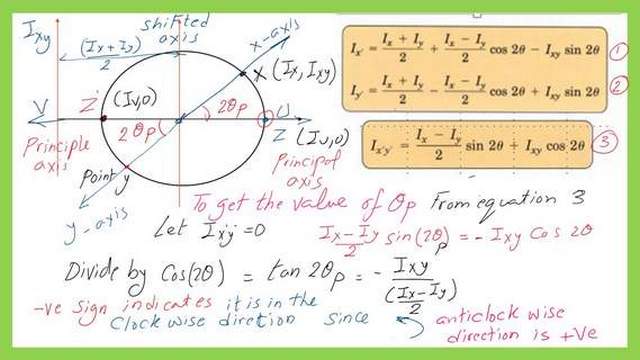

The expression of Imax using Mohr’s circle.
The value of Imax or Iu can be estimated as equal to the shift which is (Ix+Iy)/2 plus the radius value. Checking the tan 2θp expression we can draw an angle and get the radius value in terms of Ixy, Ix, and Iy.
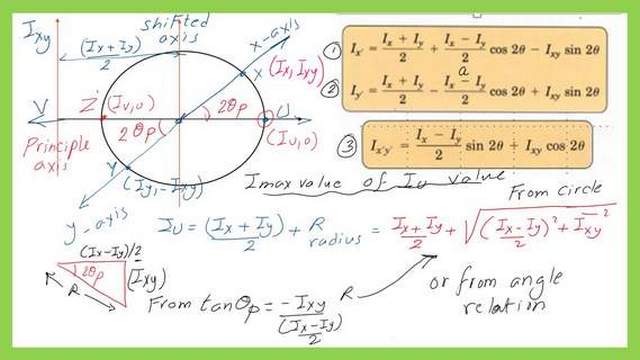

The expression of Imin using Mohr’s circle.
From the next slide in Mohr’s Circle of Inertia part-2, the value of I minimum or Imin or Iv can be estimated as equal to shift which is (Ix+Iy)/2 minus the radius value. Checking the tan 2θp expression we can draw an angle and get the radius value in terms of Ixy, Ix, and Iy and deduct the value of (Ix+Iy)/2.
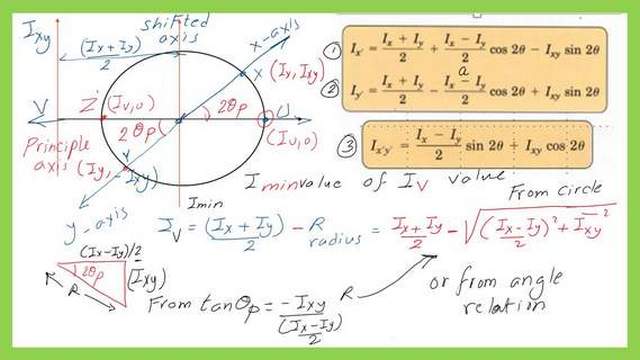

The expression of pole point.
The pole point in Mohr’s circle of inertia is the point from which you can get direction, and the center of the circle is the pole point. When we join to point x will give the X-axis.
While joining with point y you can get the Y direction similarly a line from the center of the circle to point Z will give the principal maximum direction or the U direction.
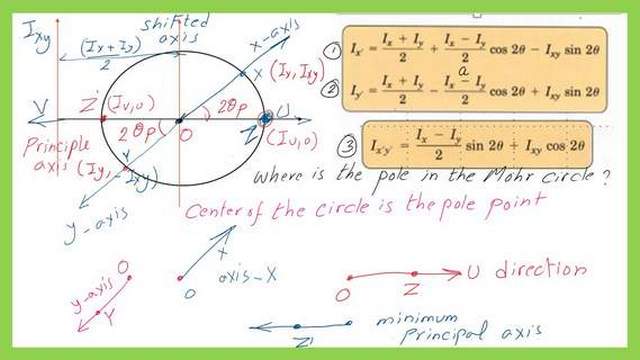

The pole point in Mohr’s circle for the normal view.
From the last slide, we can get the pole of the normal view as point Z’ joining to the mirror point of x, which will give the U direction in the normal view, and joining to the mirror of point y will give the V direction.

Thanks a lot and peace be upon you all.
This is the next post, which is titled: Easy Approach to Mohr’s Circle of inertia-First Case.
This is a link to a useful external resource. Calculator for Cross Section, Mass, Axial and Polar Area Moment of Inertia, and Section Modulus.


