Solved problem 7-2-frame K value 3/3.
Full description of the content.
Solved problem 7-2-frame K value 3/3, the un-braced portion of the frame-column GH.
We are going to continue discussing our solved problem 7-2 for frames, by God’s will, The last time we stopped by the hatched yellow color column GH, the column is an unbraced column, starting by joint H, and continue for the other joints.
At joint H no upper column, G=sum of (EI/L) which is=20.47/ sum(EI/L) for girder Gh =26.67, Gh=(20.47/26.67)=0.675.
For Gg at joint G, we have two columns GH, GF, Gc=(20.47+31.67)/sum of(m*EI/L) for girders CG and GJ, m value=1 at GC and m= 1.5, for girder GJ because of the hinge at far joint, the denominator =(1*70+1.5*21.25), Gg=0.5118. Using the French equation for the unbraced frame, with the values of Gh=0.675 and Gg=0.5118.
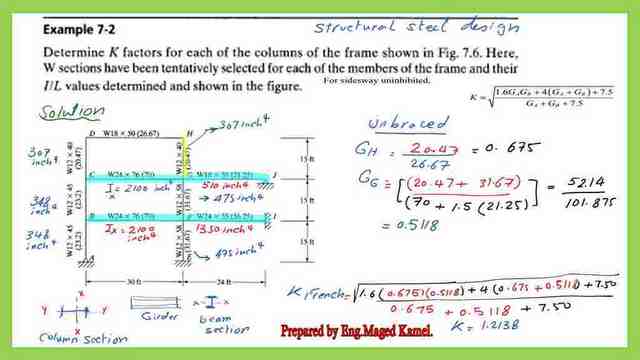

Using the Nomograph for the un-braced frame to get the K value for column HG, we have, Gleft=0.6753, G right=0.5118, The K value will be between 1.1 and 1.20 very close to 1.20.
The column Dc for the unbraced frame is also drawn in the nomograph for a side-sway un-inhibited frame.


Solved problem 7-2 for frames-part 3, column GF.
We continue estimating G for the new column GF hatched with yellow color For joint G, the joint G value as Gg=0.5118
For joint F, the G value expressed as Gf= sum(EI/L) for columns/ sum(m*EI/L) for girders, Gf=(31.67+31.67)/denominator, since m=1 for Girder FB, for girder FI is m=2 because the far end is fixed, the value of 2 is for the braced frame.
The denominator=(70+2*56.25) Gf=0.3471.
The Joint G has a girder ending with pinned support for which m value=1.50, substitute to get GG=0.5118.


Using the alignment chart for the braced frame.
Our column is GF, the point at the left Gf =0.5118, while Gc=0.3471.
The K-value from the French equation, for the braced frame, is k=0.672, while by using the Nomograph method, the k value =0.66, the k value from the French equation is quite near.


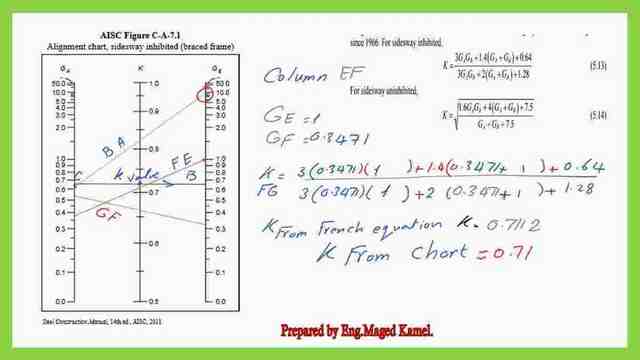
Solved problem 7-2-frame K value 3/3-column FE.
Let us continue with a new column. The last column FE, this column is braced Gf=0.3471. For point F, we have used m=2 since it is connected to a fixed support, for A side-sway inhibited frame. While joint E is fixed at the support with G value=1.


This frame is braced, using the Nomograph of the braced frame, with Gf and GE values, Ge=1 and Gf=0.3471, as we can see, the marked point, k will be above 0.70.
We consider k=0.71. While using the French equation k value for column GE, which is braced, K= ((3GA*Gb+1.4(GA+Gb)+0.64))/(3GA*Gb+2(GA+Gb)+1.28), substitute with Ge=1 and Gf=0.3471, as Ga and Gb. k=3(0.3471*1+1.4(0.3471+1)+0.64)/(3(0.3471*1)+2(0.3471+1+1.28)=0.7112.
From the French equation, the K=0.7112 which is close to 0.71 from the Nomograph chart, thus we have completed the evaluation of the k values for all the columns for the solved problem 7-2 part-2.

Solved problem 7-2-frame K value 3/3-Author solution.
I have included the solution of the author, for the solved problem 7-2 as included in the slides, as a reference for the solution, this is the table at the end, where figures of k values are closed.


This is a full detail of the value estimated by the author.


This is the pdf file used in the illustration of this post.
A very useful external link is Chapter 7 – Concentrically Loaded Compression, Members.
To check part 1 of the same example, please refer to the previous post link.
This is the next post, Stress Reduction Factor For Inelastic Columns

