Last Updated on July 3, 2025 by Maged kamel
Definition of Sets, set braces, and notations.
What is Discrete math?
Discrete mathematics studies mathematical structures that are countable or otherwise distinct and separable. Examples of structures that are discrete are combinations, graphs, and logical statements. Discrete structures can be finite or infinite.
Discrete mathematics is in contrast to continuous mathematics, which deals with structures that can range in value over the real numbers or have some non-separable quality. Refer to this link.
Since the time of Isaac Newton and until recently, almost the entire emphasis of applied mathematics has been on continuously varying processes, modeled by the mathematical continuum and using methods derived from the differential and integral calculus. In contrast,
discrete mathematics concerns itself mainly with finite collections of discrete objects. With the growth of digital devices, especially computers, discrete mathematics has become increasingly important.
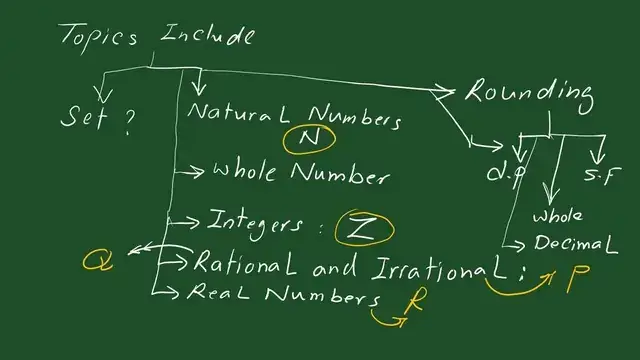
The list of items included.
The five items are included in our discussion. The first item is the natural numbers. The second item is the whole numbers. The third item is the integers. The fourth item is rational and irrational numbers.
The fifth item is the real numbers. The next step will cover how to round numbers, including decimal rounding and rounding to whole numbers and scientific figures.
Definition of sets.
What is a set? A set is a well-defined collection of objects or ideas. The sets are well-defined, a collection of objects or ideas. Elements are for which a specific condition is selected and well-defined.
For instance, we could specify that our set has x bigger or smaller than a specific value or even x = square of a number value.
What is well-defined? A set is well-defined if there is no ambiguity. Whether or not an object belongs to it, this is well defined to guarantee a correct choice for proper elements.
If the element follows the conditions stated or not for proper selection between alternatives, exclude the inappropriate choice.
A set is a well-defined collection of objects or ideas. Elements are selected based on specific conditions and well-defined criteria. For example, a set could specify objects that are greater than, less than, or equal to a particular value, or have an exact mathematical relationship.
A set is considered well-defined when there is no ambiguity regarding the inclusion of objects. This ensures a correct selection of appropriate elements by excluding non-conforming choices.

What are set braces?
Set braces: This symbol is shown as two curly brackets. The symbols are used to indicate sets.
For example, you wear shoes, socks, a hat, a shirt, pants, and so on. I quote, “I’m sure you could come up with at least a hundred.” This is known as a set. An example is a set of items that someone wears.
The following item is the notation I quote; there is a reasonably simple notation for sets. We list each element or member separated by a comma. First, we put the curly brackets.
Then, mention the well-defined element and list all the required elements separated by a comma, which satisfy your statement. If the number of elements is infinite, we can use the three dots, which means it goes on forever, just like infinity. Commas separate elements.

Three dots mean go forever. For this example, the order is not essential.

What are the whole numbers?
We begin with the definitions of terms that we discussed in the introduction. Whole numbers are simply 0, 1, 2, 3, 4, 5, and so on. The three dots signify that the numbers continue indefinitely.
In the graph, there are no fractions or negative values. For example, a set could be {0, 7, 212, 1023}. The number zero is a whole number, and so are 7 and 212, which are positive. However, 1/2 is a fraction, not a whole number.
Whole numbers do not include negative numbers, fractions, or decimals. For example, 1.1 and 3.5 are decimals and not whole numbers. The following item is a natural number.

Natural numbers are counting numbers that start from 1 and include 2, 3, 4, 5, 6, and so on. Unlike whole numbers, natural numbers do not contain zero or decimals. The next slide shows the differences between integers, rational numbers, and Real numbers.
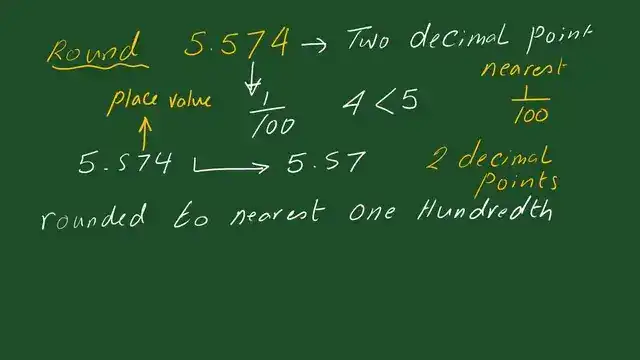
The difference between rational and irrational numbers is shown in the next slide.

Set builder illustration quoted from Math is Fun.
We will proceed to a new slide. This is the set builder, how to pronounce the expression and write it. For instance, write the left brace, then include x, then the vertical line followed by x, which is an element that belongs to, followed by the symbol N for natural numbers.

For example, x is less than 10, which means all the numbers are less than 10, and it is written as the set of all x, such that x is an element of the natural numbers and x is less than 10. 1,2,3,4,5,6,7,8,9.
We cannot increase further, so 9 is the last number. The last number is 9, less than 10. The condition is for numbers less than 10. Natural numbers do not include 0.
We start with number 1 and stop at number 9. 10 is not included because the following number will be 10, and the condition is for numbers. That is why the definition of a set is written as well-defined.
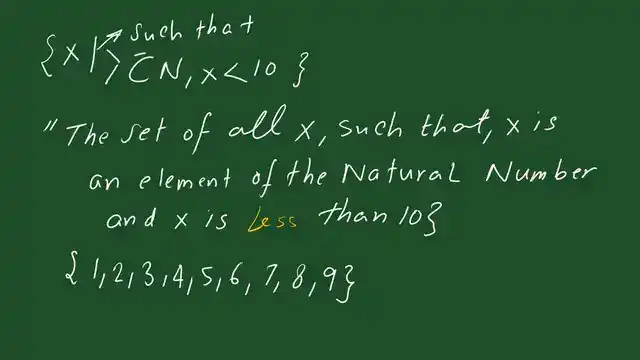
How do we express the set by symbols? In other words, symbols are assigned to the previous items we discussed.
Z plus is the symbol given for positive integers, and the vertical line means that all the positive numbers. Integers, x, can be read as x, such that the integers we will discuss shortly, just like 1, 2, 3, 4, and so on.
The symbol Z is written = then braces, followed by x, as Z=x, which is all the number of x such that x is an integer.
The Z is the symbol given for integers, which includes all positive and negative numbers and zero. Extended from the right and left, it can increase more than, be 5, 6, or infinity.
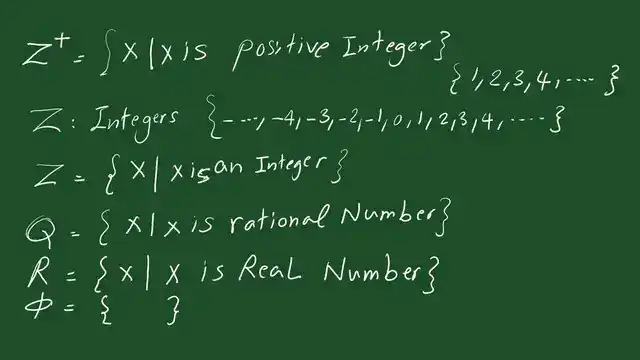
symbol Q includes the rational number, he introduces the braces and x such that x is a Rational Number.
While the symbol R is for real numbers between braces, x is all numbers such that each element belongs to real numbers. In contrast, the Φ is a symbol for all empty sets.
The set braces are located, and inside, there is nothing.

For a useful external site, try Math is Fun and an introduction to sets.
For the next post, Definition of Natural Numbers, Integers.