Last Updated on January 18, 2026 by Maged kamel
The difference between the Counting number and the Whole number.
This is the second lecture about sets. We will start by introducing solved problems. The counting numbers must be written as a set. The counting numbers are 1, 2, 3, 4, then dots. If it is required to make the whole number as we have discussed earlier, zero should be included in the set braces. The set form is shown.
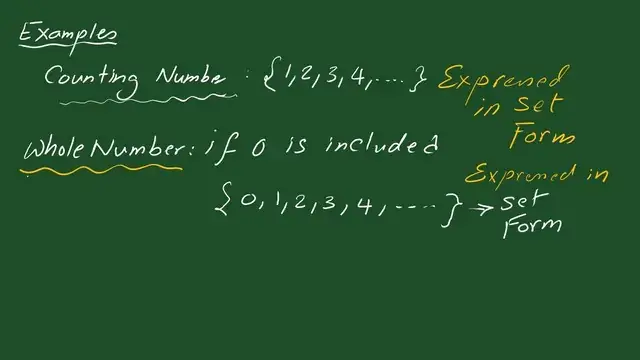
What are Integers?
We will proceed to discuss whole numbers. If we want to include the minus sign, we need integers.
The integers are like whole numbers, but they also include negative numbers.
The whole numbers start at 0 and go to infinity. Now, still no fraction or decimal, include the (+) and (-) signs, but do not include fractions or decimals. I quote, so integers can be negative (-1, -2, -3,…). They extend to infinity and include positive integers (1, 2, 3, …). The zero zero is bolded and considered a stand-alone element.
Types of Integers.
The following slide will demonstrate that when dealing with negative numbers, we move to the left, indicating -1, -2, -3, -4, and -5 dots. When dealing with positive numbers, we move to the right, writing +1, +2, +3, +4, +5. The zero will also be present in all the positive numbers.
Remember that for the negative numbers, 0 was not there. So, what numbers are missing? These numbers are + and 0, so when saying nonnegative.
We have to include 0 and +ve numbers. Suppose we need to include non-positive integers.
The zero should be there, as should all the negative numbers. 0 is a standalone element and is included while excluding non-negative Integers or non-positive integers.
Solved problems 1 and 2.
We will check another solved problem: Which one of the following is not a whole number? Four answers were given: +5, +10, -3, +8. The correct answer is C -3 is a negative number and thus not a whole number. C is the correct answer because it is not a whole number, as it is negative.
For problem 2, which of the following is not a number? 10, 2, 8, 1/4. The integers include zero and positive and negative numbers; non-integers are fractions or decimals. Option D is not an integer, A is a negative integer, and B and C are positive integers. d is selected.
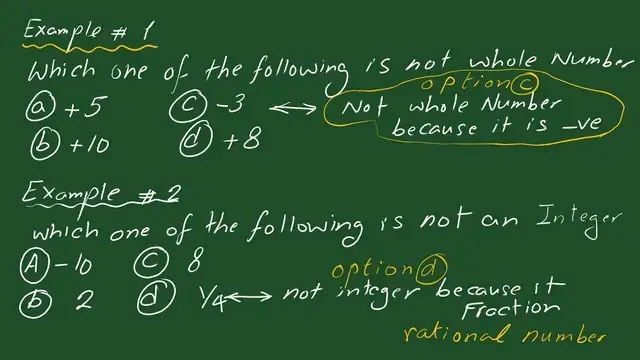
Solved problem-3.
For solved problem-3, which of the following describes the given set? {…, -5, -4, -3, -2, -1, 0). The dots show that we have negative numbers going to infinity; if we read, we have 0, -1, -2, -3, -4, -5.
We need the expression that describes the content of the set. This justification for the set builder has four options; we need to select one of these choices, which is correct. The first choice states that the set consists of negative whole numbers.
The second choice states the set is Non-(+ve) numbers. The third choice states the set is of -ve numbers. The fourth choice states that the set is non-negative numbers. For the first choice, a set is a negative whole number. There are no negative whole numbers.
The entire set of numbers is (0, 1, 2, 3, 4, 5,…). For the second choice, the set is the set of non-positive numbers. For non-positive integers, this choice is correct, since they include 0 and negative numbers. For the third choice, the set is of negative integers.
What are the negative integers? The negative integers include all negative values of numbers to infinity, but this does not contain zero, which is not true of the given set.
This statement holds true if the given set excludes zero. For the fourth choice, the set is of non-negative integers. This statement is wrong, since the set includes zero and all negative numbers. The correct answer is b, which is the set of non-positive numbers.
Solved example -4.
For solved problem number 4, he draws a line from 0 to 5. And also draw -1, -2, -3, -4, -5 Q letter is placed at -4, the letter A is at -2.50, letter B at -1, and letter B’ at 0. Letter F is at +1, letter C at +2.5, and letter D at +4.
Letter E is at +5. From the figure, how many positive numbers are more than negative ones? The positive numbers should be greater than the negative numbers, but by how many?
The four options were given. Let us check together so you can participate in the answer and see why we chose c as the correct answer: 1. For +ve numbers, there is no decimal or fraction, whether +ve or negative, so we will exclude the fraction items since the value = -2.50.
We will exclude c since it is +2.5. How many positive letters? We have F, d,e. Again, how many negative letters do you have with no fraction or decimal? We have B, Q.
So 3-2=1, then c is the correct choice. Check the analysis now. A is not a number since it is a fraction. c is not an integer, we have -2.50 B’ is zero. Not Positive, negative, or nonnegative. The positive figures are F, d, and e. The negative figures are B and Q.
Solved problem -5.
Example 5: Which of the following is correctly described? The set of the whole number is written as {…, -4, -3,-2, -1,0 }. The first option is to set the whole number to less than 4.
The second option is the set of whole numbers <= 4. The third option is the set of the Integers, which is <= 4.
If we said that a set is a whole number, this is not true, since the set of whole numbers includes all positive integers.
The first two options are not valid. We are left with I,
We have two options: the set of Integers <= +4 or >= -4 and <= 4? Let us check option number no.4.
If we choose this option, we will select the positive and negative Integers.
If we select option 4 for >=-4 and Less = 4, it will give us a set of this form extending from 4 to -4. Since it is an Integer, it contains both positive and negative. However, our given set extends to negative infinity.
Selecting option 4 will not yield the correct set, as our last term will be -4. The proper solution is option 3. For review, we first checked that the given set is not a set of whole numbers. Then select the right option between 3 and 4.
The PDF data for this post can be viewed or downloaded from the following document.
For a useful external site, math is fun and provides valuable data on whole numbers and integers.
For the next post, the Definition of absolute value, rational numbers, and fractions.