Full detailed illustration of the Moment of inertia Iy for a triangle.
Full detailed illustration of the Moment of inertia Iy for the triangle.
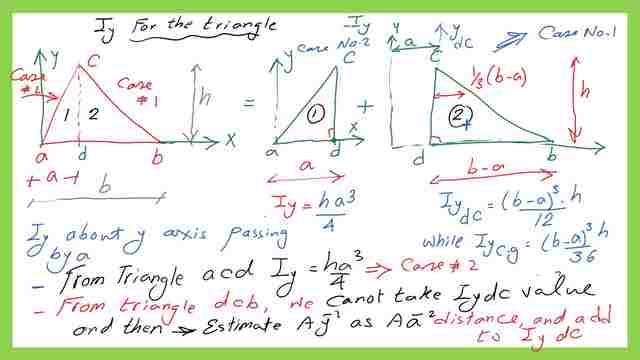
We aim to get the moment of inertia Iy for the triangle at the y-axis, passing by point a.
1-Since the triangle ABC consists of two triangles ACD and DBC, for the inertia of the triangle we are going to add the sum of two inertias for those two right angles about the same axis y.
2-The inertia for an angle adc about axis y passing by point a=Iy1=h*a^3/12, where a is the base of the triangle ADC and h is the height. recall this value was estimated for the right-angle case no-2. 3-The inertia for an angle dbc about axis y-dc passing by point d=Iy-dc=(b-a)^3*h/12/12, where b is the base of the triangle abc.

We have to estimate the inertia at the Cg for right angle triangle case 1 and from Cg we can proceed to evaluate the inertia at any place.
4-For the second triangle dbc, we need to estimate Iy-CG , then we add (area*x bar^2), the area is the area of the triangle dbc, x bar is the distance from its Cg t axis Y.
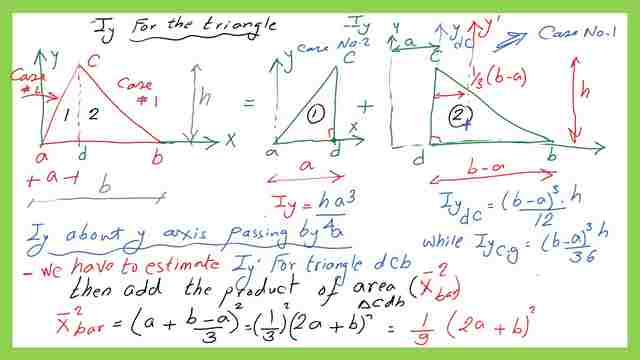

5- x bar distance as shown in the next slide, x bar=a+(b-a)1/3=(2/3)a+(b/3).
6- x^2-bar can be wriien asxbar^2=(1/9)*(2a+b)^2.
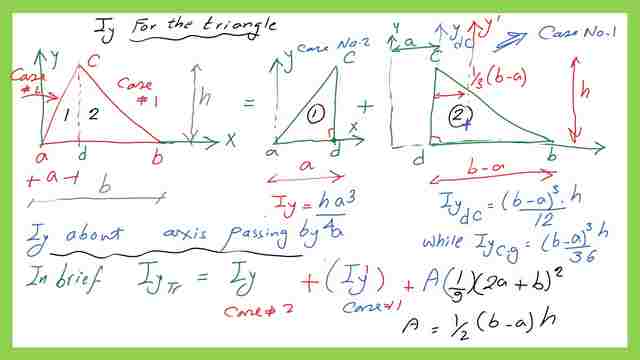

The final value of Iy-Iy final=Iy case -2 triangle+ Iy-cg for triangle dbc+A*x^2 bar.
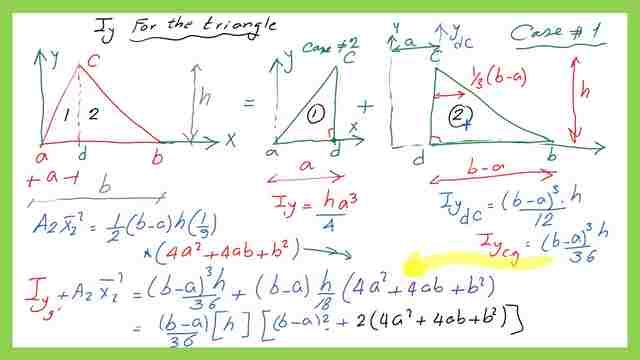

In the following images, there is more details of the summation process for Iy.
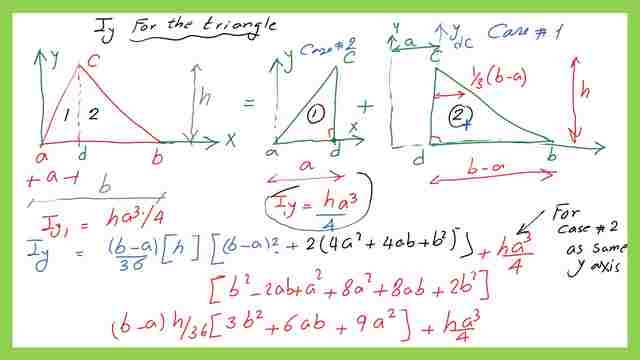

7-We substitute all the known values obtained earlier, the expression can be shown in the next slide image.


The radius of gyration for the triangle about axis y for the triangle.
From the value of Iy by the area of the triangle, then take the square root of the product, then the value of ky can be found.
This is the final value of k^2y for the triangle.


We have completed the estimation of inertia Iy for a triangle and we can check the result by comparing the inertia value with the NCEEs table.
This is the list of inertia for triangular shapes quoted from the NCEES tables of inertia.
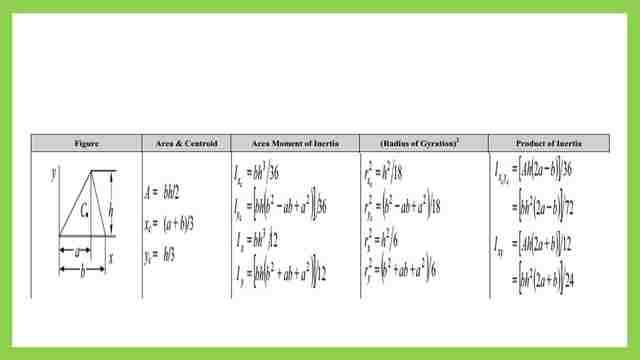

This is the pdf file used in the illustration of this post.
For an external resource, the definition of the moment of inertia with solved problems, 2nd moment of inertia.
This is the next post, How to get of Moment of inertia Iy-at Cg for a triangle?

