Last Updated on February 18, 2026 by Maged kamel
A solved problem 7-4-1 is introduced, in which the design of a steel beam requires selecting the lightest W or M section under given uniform dead and live loads. Two cases are presented for two different values of Fy. The first case is for A36 steel, while the second case is for A572 grade 50 steel.
How to design a steel beam? Solved problem-7-4-1.
This is the first part of the post on designing a steel beam using various steel types. In this first part, we will consider Fy = 36 ksi and Fy = 50 ksi. The second part of this post will consider A572 steel.
How to design a steel beam? Solved problem-7-4-1.
A steel beam with the lightest W or M section must be designed under a uniformly distributed load and a given live load. The beam’s compression flange is fully supported against lateral movement.
For Case#1- Design a steel beam with Fy=36 ksi.
For the first case of the yield stress of Fy=36 ksi, it is required to design a steel beam of W—section or M-section for a simply supported beam of span =20′ for the three cases of Fy values.
Find the Ultimate Moment-Fy=36 ksi.
Starting with ASTM A36, where the Fy=36 ksi. The first step in designing a steel beam is to estimate its ultimate load capacity, 1.20D + 1.6L. The ultimate uniform load, ultimate uniform load, Wult=1.2*0.20+1.60*0.80=1.52 kips/Ft. The ultimate moment for a supported beam, Mult= wult*L^2/8. Mult=1.52*20^2/8=76 Ft.kips. This is the value of Multimate.

A reminder of the corresponding Fy values for A36 and A992 from Table 2-4.

Determine the required Zx-select a section.
Our first trial is to equate Mult/(0.90*Fy) to Zx, determine the plastic section modulus Zx, and then check Table 3-2.
The next slide shows the limiting slenderness parameters λF and λw for ASTM A36, where Fy=36 ksi, λFp=0.38*sqrt*(E/Fy)=0.38*sqrt(29000/36) =10.79, while flange λFr=1*sqrt*(E/Fy)=28.38. For web lambda λwp=3.76*sqrt(E/Fy)=106.72, whie for lambda λwr=5.70*sqrt*(E/Fy)=922.141.
The plastic section modulus equals 28.15 inch3.

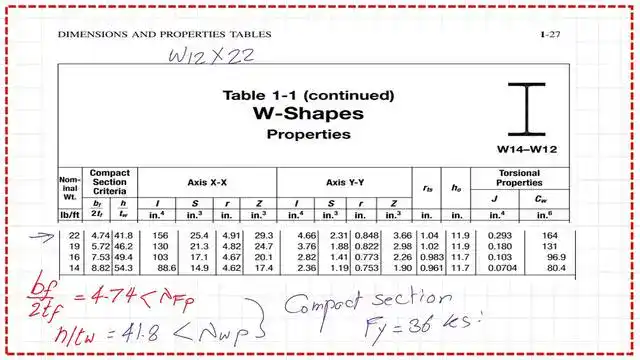
We will use Table 3-2, where Zx sorts W sections. We find that W12x22 has a Zx value of 29.30 in^3; the Zxc value exceeds the required Zx.

Flange λ and web λ against local buckling parameters.
We will get the slenderness ratios for both the flange and web, and the flange lambda λF and lambda λw for the selected W12x22 beam from Table 1-1 and compare these values with the limiting values of lambda λp; based on the comparison, we will determine if lambda λF or lambda λw< lambda λp – plastic. From Table 1-1, in the second part, the flange λf = 4.74 and the web λ = 41.80.
The next slide shows that section W12x22 is compact.
What about lateral torsional buckling?
For lateral torsional buckling, the compression flange is fully supported against lateral movement. The section is safe against lateral Torsional buckling. The subject of lateral torsional buckling will be discussed in post 10.

We will readjust the value of the ultimate moment by adding its weight—the new Mult=1.555*20^2/8=77.32 ft. kips for the selected section W12x22.
Since our selected section is compact, Mn = Mp. Zx=Fy*Zx. For the LRFD, the value of Φb*Mn=Φb*Fy*Zx, which is Φb*Fy*Zx=79.11 Ft.kips.
Since the acting Multimate is only 77.32 ft. kips, the section is safe since 79.11 Ft. kips is >77.32 ft. kips.

For Case #2, design a steel beam with yield stress Fy = 50 ksi.
Determine the required Zx-Fy=50 ksi.
The second case for ASTM A 992, where Fy=50 ksi. Mult without the superimposed load was 76 ft-kips.
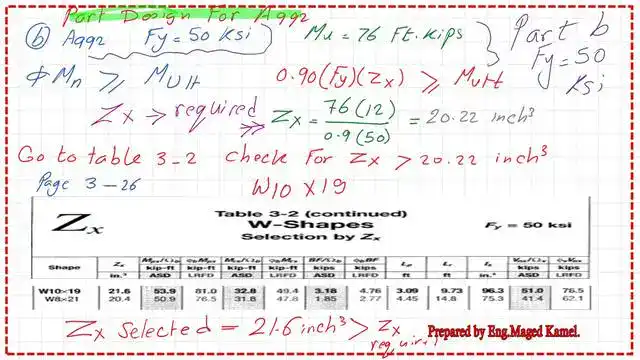
We need Zx to start with Table 3-2. Zx=Mult/(0.90*50)=20.22 inch3.
We will proceed to table 3-2, but select Zx > 20.22 in^3; this corresponds to W10x19 with Zx = 21.60 in^3. Zx selected=21.60 inch3. We proceed to get the properties of our section. W10x19.
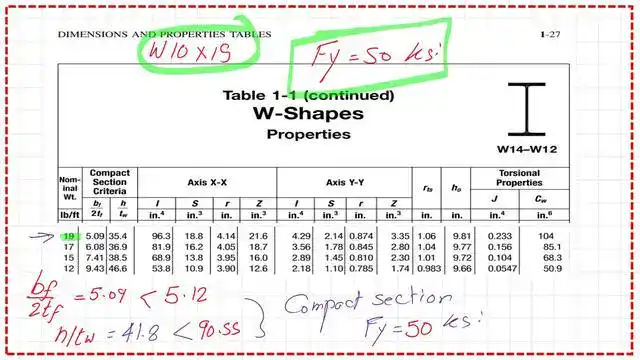
The required Local buckling parameters for Fy = 50 ksi.
On the next slide, we determine the local buckling parameters for the Flange and Web, based on Fy = 50 ksi.

From Table 1-1 part 2, the λ for flange equals 5.09, which is <λfp, and the λ for web is smaller than λwp, and the section is compact.
For the Mult, we will adjust it due to the superimposed load and the beam weight (19 lb/ft), and the final Mult = 77.14 ft ·kips.
The Φb*Mn=81.00 Ft.kips >Mult. The compact section is the final step in designing a steel beam with Fy = 50 ksi. This is the end of part 1; part 2 will follow with the design of a section when Fy = 65 ksi.

The PDF file for this post can be viewed or downloaded from the following link.
The continuation of this post is in the next post: 9A-9A-Solved problem-7-4-1-part 2.
Here is the link to Chapter 8, “Bending Members.” A Beginner’s Guide to the Steel Construction Manual, 14th ed.
Here is the link to Chapter 8: Bending Members. A Beginner’s Guide to the Steel Construction Manual, 15th ed.
Here is the link to Chapter 8: Bending Members. A Beginner’s Guide to the Steel Construction Manual, 16th ed.
This links to the next post, 10-lateral-torsional buckling for steel beams.