Last Updated on December 31, 2025 by Maged kamel
Moment of inertia for right-angle-Ix-Case-1.
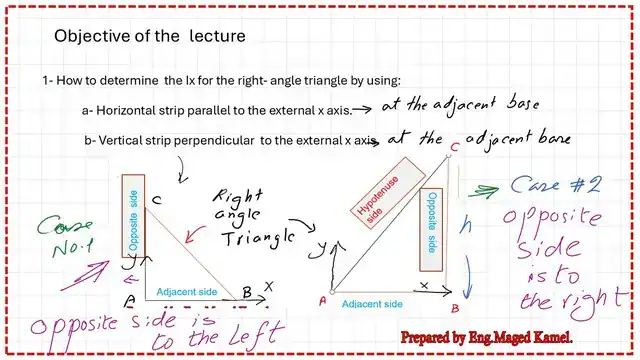
What is the difference between case 1 and case 2?
Case no.1 is the one for which the x-axis coincides with the base and the y-axis coincides with the opposite side, while case no.2 is the one for which the x-axis coincides with the base and the y-axis is at the intersection point between the adjacent side and the hypotenuse side.
For Case no. 1, the moment of inertia for right-angle-Ix is the second case in the attached reference table from the FE Exam reference manual 3-5. While case 2 is the first case in the same table. This is the list of the first moment of area and inertia for the common plane shapes.
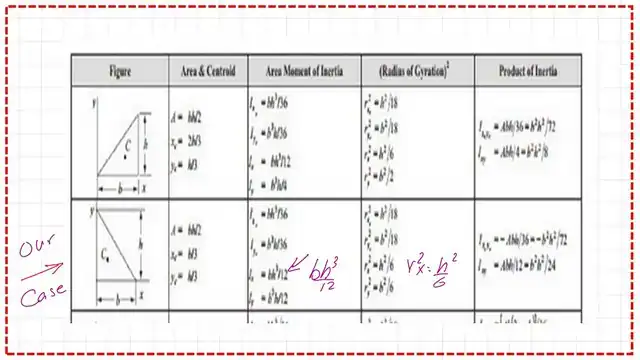
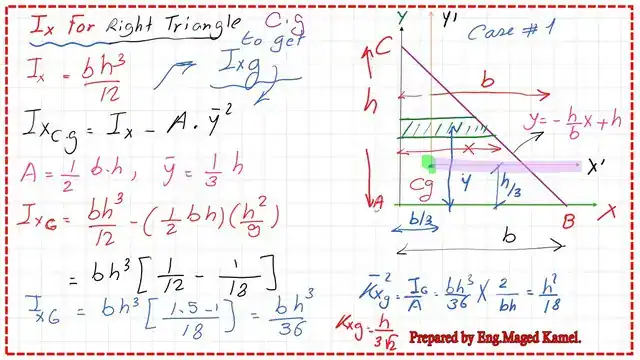
The next slide image shows the difference between Case-1 and Case-2 of the right-angled triangle. For case -1, the opposite of the triangle is on the left side, and for case-2, the opposite of the triangle is on the right.
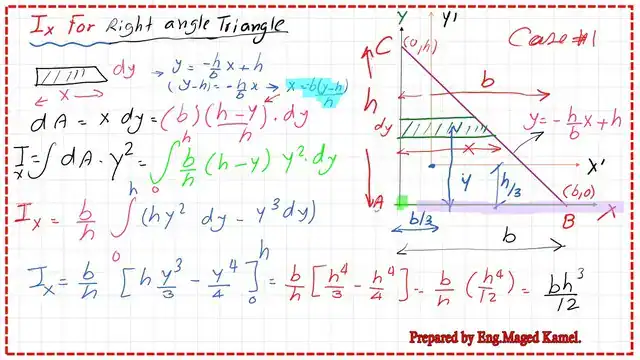
How can I get the inertia for a right-angle Ix using a horizontal strip?
For an x-axis passing by the base and the Y-axis passing by the left side, using the following steps, we will estimate the inertia for right-angle-Ix using a horizontal strip:
For line CB, we will write the equation for that line as y = (-h*x/b) + h.
We can check the validity of this equation by substituting the x-coordinates of both C& b and getting the corresponding y-values.
2- Our strip is a horizontal strip with width=dy and base=x.
3-dA, which is the area of the horizontal strip, will be equal to the base multiplied by the height, x*dy. To get the dy, we will differentiate the y equation, which we have already estimated.
4- Our moment of inertia due to the strip is dIx=dA*y^2, remember that dA=x*dy.
5- We can write dIx=b*(h-y)/h*(y^2*dy), after substitution by the value of dy.
6-the value of Ix=∫dIx=∫b(h-y)/h(y^2dy), from y=0 to y=h.6- after integration and substitutionwe get Ix=bh^3/12.
The value of inertia for a right-angle-Ix=base*height^3/12. The following slide image shows the steps.
How can I get the inertia for right-angle-Ix using a vertical strip?
Using the following steps, we will estimate the Ix, the moment of inertia for the right-angle triangle by using a vertical strip:
1- We are going to move this strip horizontally, so we have to substitute the value of y=-h/b*x+h, as we will see later.
2- Our strip is a vertical strip with width=dx and height = y.
3- The strip with an area dA, will be=y*dx.
4-The moment of inertia for the small element -dIx from our study of a rectangular section can be estimated as dx*y^3.
5- The moment of inertia for the small element – dIx value is shown as per the next slide picture.
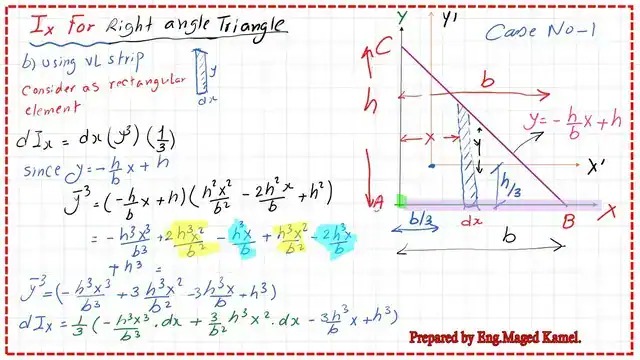
6-Integrate from x=0 to x=b.
7- We will get the same value of Ix as estimated by using a horizontal strip, which is=bh^3/12.8- k^2x=Ix/A=bh^3/(12(0.50b*h))=h^2/6.
How to get the inertia for a right-angle Ix at the CG?
To get the inertia for right-angle-Ix at the CG, we can use the expression of Ix and then find Ixg at the CG from the theorem of parallel axes, by deducting the product of the area by the square of the distance between the CG and the X-axis.
The moment at the CG, Ixg=Ix-A*ybar^2. Substitute by the value of Ix, write Ixg is equal to (b*h^3/12)-(0.50*b*h)*(h/3)^2=Ixg=b*h^3/36. The radius of gyration at the Cg, Kxg=sqrt(IxG/Area)=sqrt(bh^3/36)/(0.50bh))=h/(3*sqrt(2)).
This is the PDF file for the content in the post.
This is a link to the next post, ‘Moment of Inertia – for the Right-Angle Triangle Case 1-Iy.
This is a useful external link for the moment of inertia- The Moment of Inertia of a Rectangle.
This is a link to the video that accompanies this post.