8-Moment of inertia-Iy for right-angle triangle-case-1.

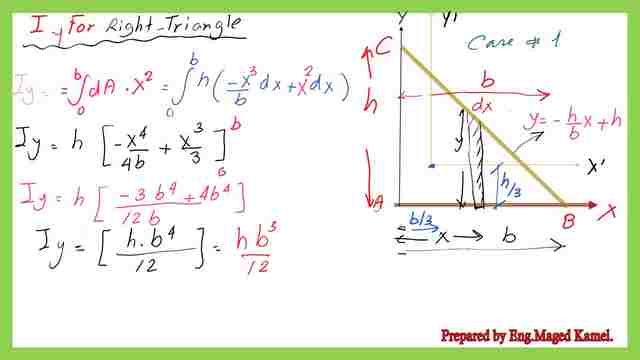
Moment of inertia-Iy for the right-angle triangle-Case-1.

Step-by-step guide for the calculation of moment of inertia-Iy right-angle-case-1.

We are interested in the left corner of that triangle again our expression of the line BC is y= (-h/b)*x+h, for the vertical strip, its area is dA, and we have dA= the width which is dx*y.

We will integrate the value of X from X=0 to X = b. We substitute for the Y- value by writing the equation of y=(-h*x/b)+h, our dA *x^2 will give the value of dIy about the y-axis. Multiply dA*x^2. The expression for dIy=(h*)-(x^3*dx/b) +x^2*dx).

The integration from x=0 to x=b will be carried out.

Finally, the value of the moment of inertia about the Y axis, Iy=h*b^3/12, for which, h, is the triangle height and b is the base length. the inertia is about the y-axis on the left side of the triangle.

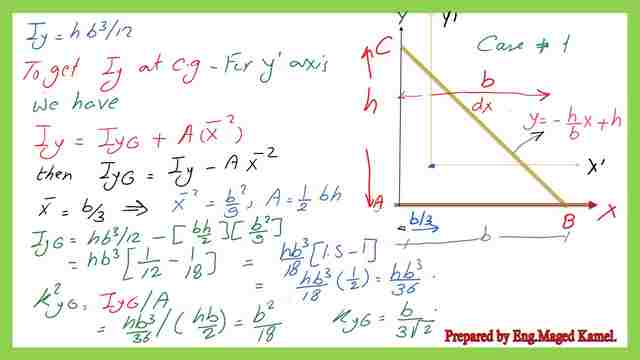
Moment of inertia-Iy at the CG of the right-angle triangle.

For Iy at the CG, we will use the parallel axes theorem and deduct the product of A*xbar^2. x bar represents the horizontal distance between Cg and the vertical axis Y.

The area A=(1/2)*b*h, for the triangle Cg is located at a distance=b/3 from the left corner and y=h/3 from the base of the triangle. Finally, we get Iyg=h*b^3/36.  The square of the radius of gyration k^2y can be estimated by dividing Iyg/A. The value of K^2yg equals b^2/18.

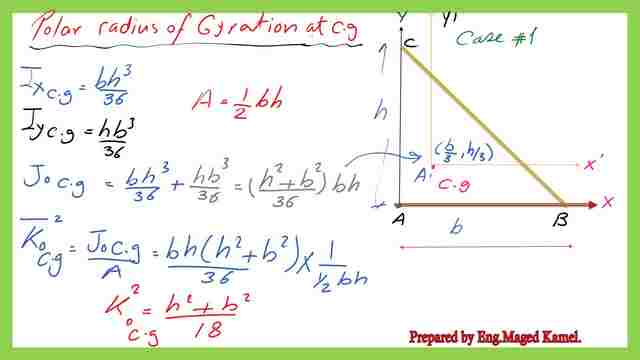
Polar moment of inertia at the CG for the right-angle triangle for case-1.

Polar moment of inertia for the right-angle triangle case-1, at the Y-axis passing the CG. We have estimated Ix at the CG, from post-7-Moment of inertia for right-angle-Ix- Case-1.

The polar moment of inertia Ip=Ixg+Iyg, adding them together, then Ipg=b*h(b^2+h^2)/36, we call it Jog, the value at Jog at the CG is shown as per the next slide image. The final value of J0 at Cg=(h^2+b^2)/18

Polar moment of inertia at the left corner for the right-angle triangle for case-1.

The Polar of inertia at the external axis x,y passing the external corner. Jo=Ix+Iy, adding them together, then Jo=b*h(b^2+h^2)/12. The value at Jog at the CG is shown as per the next slide image.

Using a horizontal strip as one option to estimate the moment of inertia-Iy value.

The new option is to use a horizontal strip to get the value of the moment of inertia-Iy for a right-angle triangle case No-1. The following steps are followed: 1- establish a relation between x and y, where x is the strip width, while y is the distance from the base to that strip, this can be done by examining the slope of line CB.

2-What is the inertia of that strip about the y-axis? the answer is that this is a typical case of a rectangle section moment of inertia Iy at the edge, which is equal to the height of the width^3. We can substitute and use the relation between x and y.

We are integrating into the y-direction, we want to get rid of x.

3-The integration will be done from y=0 to y=h. Finally, we can get the Iy value or the moment of inertia Iy for a right-angle triangle case-1 about the Y-axis. The result is matching with the previous value of Iy. However, this method took a longer time compared with the vertical strip.

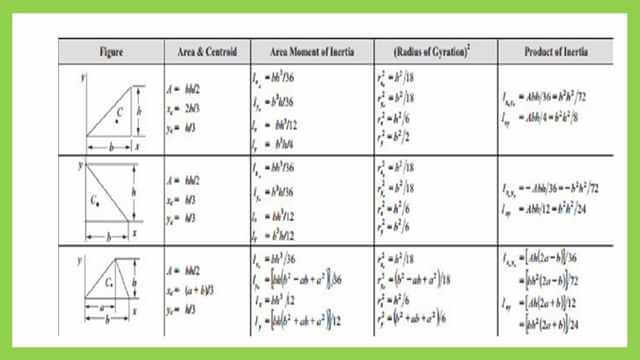
As we can see the final result matches the values included in the table of inertia for plane shapes.

This is the PDF used for the illustration of this post.

This is a link Second Moment of Area for Standard shapes.

This is the next post, Product of inertia Ixy– for the right-angle triangle-case-1.