- The Plastic Moment For Continuous Beams.
- The plastic moment for continuous beams by the Upper bound theorem.
- What is the external work for a uniformly distributed load on a simply supported beam by the upper bound theorem?
- What is the plastic moment for continuous beams under uniform distributed load at the end span?
- What is the plastic moment for continuous beams under uniformly distributed load on the Intermediate span?
The Plastic Moment For Continuous Beams.
The plastic moment for continuous beams by statical method theorem.
How to estimate the bending moment for the continuous beams?
We can estimate the bending moment by using the statical method or by using the Kinematic method or the virtual work method.
For the end span, we have one roller support having one reaction and at the other end fixed support that has three reactions, adding them together=3+1=4, we have 3 equations of equilibrium.
The sum of X=0, the sum of Y=0, and the sum of moments=0 deduct these equation numbers from 4, and we get 4-3=1, then the system is converted to a statically determinate. We will deduct 1 to convert the system to an unstable system.
The number of plastic hinges=3+1-3+1=2, the proposed location for the first hinge is at the fixed support, the second plastic hinge will be apart by x distance from the roller support.
We have a positive moment of the first span is a parabola, we assume that the hinge is apart by distance x from the left support, as a reminder of this method, we have a negative moment Mp and there is a positive Mp, for which we lay the two diagrams together.
We will deduct, I will draw another sketch to show it much clearer, this Mp a negative moment, we join the value to zero, then draw the parabola as a value of W*L^2/8.
We do not know the exact location of the plastic hinge, in the first span, or whether it is located in the mid-span, in that case, the Mp +ve value will be (W*L^2/8-0.50*MP).
The remaining ordinate is the Mp positive value.
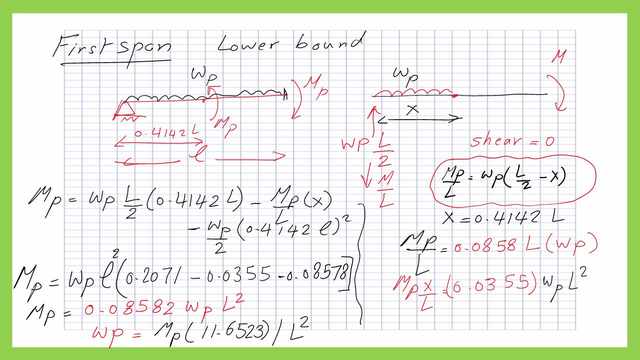
The end span can be represented by two spans, the first span is loaded under w /linear distance, and the second span is subjected to moment M acting on the right support, in the clockwise direction. For the reactions, they can be considered as the superposition of the two spans, for roller support, RA=w*L/2-M/L.
While for the other support b, RB=w*L/2+M/L.
For M= Mp at the end support, the moment at distance x from the left support, the moment from reactions- moment from the uniform loading Mx=RA*x-w*x^2/2-Mp/L*x.
This moment at the plastic hinge should = Mp if this point is the exact location of the plastic hinge.
Note that for any other location, Mx will not be=Mp, we will differentiate with respect to x.
Consider w=wp since we are estimating at the collapse stage. dM/dx=0, 0=wp*L/2 -2*wp*x-Mp/L, then, Mp/L=wp*(L/2-x), then Mp=wp*L(L/2-x) as equation number 2. Let Mx= Mp in equation Number1, we will substitute by the value of Mp/L.
In the next slide, back to equation no.1-Mx=Wp*L*x/2- wp*x^2/2-(Mp/L)*x, where Mp=wp*L(L/2-x).
Let Mx= Mp,( Mp+Mp*x/L)=w*P/2*(Lx-x^2).wp will be eliminated by wp, L goes with L, Multiply by 2, and readjust the terms.
Finally, x^2+2x*L-L^2=0 is a second-degree formula for which the x value, where x is the distance to the plastic hinge from the left support. X value= -L+-sqrt(2)*L, x value =0.414 L, not in the mid-span.
To get Mp value we will substitute it with the value of x=0.414*L, Mp=wp*L(L/2-0.414L)=wp*L(0.086). This is the value of Mp, which is the value of the Plastic Moment For Continuous Beams at the end span in terms of the plastic uniform load.

The plastic moment for continuous beams at the Intermediate span.
While the intermediate span, which has a uniformly distributed load wp, can be represented by a span with two end moments each moment value of Mp with a uniform load =wp.
We are still dealing with the lower bound theorem, 2Mp=Wp*L^2/8, the Mp=wp*L^2/16, then the load at collapse wp=16*Mp/L^2.
This value is bigger than the Mp value estimated at the end span.
The third span is symmetrical to the first span and the Plastic moment value will be the same.
The plastic moment for continuous beams by the Upper bound theorem.
What is the external work for a uniformly distributed load on a simply supported beam by the upper bound theorem?
First, let us derive a relation between the Uniform load w and the external work due to that load for a simply supported beam of length L. If we divide the beam into two halves then the total external work will be twice the work created for one half, considering as if the uniformly is a concentrated load =w*l/2. For work multiply w(l/2)Δ/2=W(L/4)Δ. So the total work is due to a uniform load on a beam We=2W(L/4)Δ=0.50WL. Δ or half the spanUl*delta.
What is the plastic moment for continuous beams under uniform distributed load at the end span?
To get the plastic moment for continuous beams for the end span but, by using the upper bound theorem.
We will create a mechanism. We will assume the plastic hinge is located at a distance x from the left support, the remaining distance=L-x to the right support.
For the deflected shape, at the plastic hinge, the deflection value is Δ at x distance from the left support, the Moment at the right support =Mp, and there is another moment Mp+ve at the plastic hinge.
We equate the external work with the internal work, Wp*(L/2)*Δ=Mp*β+Mp(α+ β), α=tan α=Δ/L, β=Δ/L-x,α+β=(Δ/x)+(Δ/L-x).
Checking the equation, we have Mp*( α+2*β).
We combine all together (α+2*β)=(Δ/x)+2*Δ/(L-x)=Δ(L-x+2x)/(x)*(L-x)=Δ(L+x)/(x)*(L-x). We substitute in the equation for external work, wp*L/2*Δ=Mp*Δ(L+x)/(x)*(L-x),Δ goes with Δ, then Mp=wp*L/2*(L-x)/(L+x).
We could make a table to draw the relation between x and Mp in the form of a diagram, instead of plotting and giving different values of x, for each increment, say x0=0.10L,x1=0.20L, etc, and get the corresponding Mp value in return.
Since the graph will have a minimum point for which the slope =0.
We will differentiate dMp/dx=0, and the laws of differentiation for a fraction will be used, we continue till we get the x^2+2x*L-L^2=0.
The value of x=0.4142*L, this the same result we have obtained by using the statical method or the lower bound theorem.
We will substitute by the value of x in the relation of Mp, by x=0.4142*L, then, Mp value= 0.08578 *wp*L^2, which is the value of the Plastic Moment For Continuous Beams at the end span.
We have satisfied the three conditions which are equilibrium, mechanism, and, uniqueness, as there is no higher value other than Mp, by using differentiation.
What is the plastic moment for continuous beams under uniformly distributed load on the Intermediate span?
The last requirement for the interior span is to get the Mp values by using the upper bound theorem.
We will get the same result for Mp=wp*L^2/16, which is the value of the Plastic Moment For Continuous Beams at the intermediate span, which is similar to the lower bound theorem result, so we get a unique solution obtained.
We have completed the estimation of the plastic moment for continuous beams of three equal spans under a plastic uniform distributed load.

This is the pdf file used in the illustration of this post.
For useful link about the structural analysis -III.
This is the next post is Solved Problem 8-22 For Plastic Moment.

