Stiffness reduction factor for inelastic columns-part 2.
In the previous post we talked about the difference between Fcr from the Euler graph and the Fcr for inelastic columns, please refer to this link for review.
How do we get the expression of the Stiffness reduction factor for inelastic columns?
Prof. Segui has introduced various equations to get an expression for τb, using Fcr inelastic term.
Using the λ^2=fy/Fcr elastic then *(Fcr inel/Fcr inelastic), use the τb= Fcr in/Fcr elastic then we get λ^2=τb*(fy/fcr inelastic).
We get The final Expression τb the stiffness reduction factor τb = 4*(Fcr/Fy)*(1-Fcr/Fy).
If we use the stresses expression, in terms of loads, the stiffness reduction factor will be τb =4*(Pn/Py)*(1-Pn/Py), Pn=Fcr*Ag, Py=Fy*Ag.
The previous expression was further modified by the load which can be expressed in the LRFD or the ASD, another α factor was introduced.
In the case of LRFD, the α factor =1, and for the ASD, α factor =1.6. This is the code provision First check that α*Pr/Pns <=0.50. If we use Pns, this is considered =Py in all cases, α factor =1 for LRFD, Pr=Pult=1.2 D.L +1.60L.
In the case of ASD then Pt=Pd+PL, refer to τb equation, for the pr expression (α*Ppr)=(1*Pult)=(1*Pult), the Pns =Py, in case of ASD,(α*Ppr)=(1.60*PT).
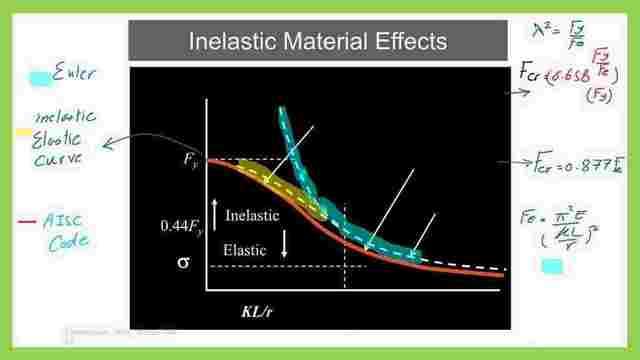
The new slide shows various types of curves, quoted from the Umass link, which has a very useful illustration for the compression steel members, the blue curve is the Euler curve, and the dotted curve in yellow is the inelastic column curve, which it has Et<E.
While the brown color curve is the Aisc code provision for inelastic columns Fcr equation, can be divided into two parts. In the first part, the elastic columns, where Kl/r>4.71(sqrt(E/Fy).
Fcr=0.877 Fe, Where Fe is the Euler stress from the Euler equation. when K*L/r<=4.71(sqrt(E/Fy), Fcr=0.658^(Fy/Fe) *Fy, then consider Fy/Fe=λ^2.
This is the table, 4-13, used to get the value of stiffness reduction factor for inelastic columns τb, the table is divided into the upper row for the different values of Fy
On the other left side of the table, Pt/Ag, as in the case of ASD case if Pt=Pd+Pl, and in the case of LRFD, we use Pult/Ag.
This is a link for the pdf file used in the illustration of this post.
A very useful external link is Chapter 7 – Concentrically Loaded Compression Members.
The next post will be a solved problem 4-13 for the stiffness reduction factor.