Last Updated on March 21, 2024 by Maged kamel
Definition of absolute value, rational numbers, fraction.
What is the absolute value of a number?
This is a review of the information about the absolute value, which is usually written for any number enclosed by two small vertical lines, which is the absolute value of ABS of -4=4. If we draw a number line, with equal distances, writing from 0 to 5 till infinity, and from the left side, we write (-1) to (-5) to infinity Absolute means How far from zero.
For any number regardless of being positive or negative. When someone needs to know about the distance for any given number from zero. The answer will be 4 or 5 or 6 depending on that number. The absolute value of a number is the distance for that number from zero. We will not say(+4) or(+5), you will write a number without a sign, then the distance for the ABS of (-4), there are 4 spaces from the zero, which is the same distance for the positive value of 4.

The fraction of a number.
Then the rational number is(1/5). But if the denominator is zero, we get infinity, when dividing any number by zero.

The fraction of numbers like 1/2,3/4, and 7/10 are the family of fractions, the upper part is called the numerator and the lower part is the denominator. The fraction can be divided into parts, the first part is the proper fraction. If the denominator value is > the numerator value, this will give a value <1.

If we have the reverse when the numerator is > denominator, for instance, this will give a value >1. Like (4/3) and 6/3=2 and 8/5 will give 1.60. The second type is called an improper fraction. While the first type is called proper fraction. The next slide images explain the definition of fractions and the various types of fractions, quoted from Basic College Mathematics by Prof. Aufmann.

What is factoring?
The product and factoring When we have x^2 +4x +2, and it is required to make factoring, we can say (x^2+4x+2) its factor = (x+2)*(x+2), which means that it is returned into its major elements when multiplied we get the original element. For instance number 12, its factors are (112),(34),(2*6). These elements when multiplied will get 12. For elements, a and b when multiplied we will get c.

Then c is the product due by multiplying two factors a and b. Product is due to the multiplication of can be back to elements by factoring. What is an Irrational number? We have said that every number is a ratio.
Integer 5 can be estimated as the ratio of 5/1. Also, 7 can be written as 7/1, which is an Improper fraction.
Irrational numbers.
What are the irrational numbers? these numbers are real numbers that cannot be written as simple fractions. We use the calculator to get the square root of 3, we get 1.732050808.

While the square root of 2 is 1.41412135. Pi is an example of an irrational number, its value=3.14159, and continues to infinity.
Non-terminating -Non -recurring decimal. Non- Terminating item, to give an example of terminating number 1/2=0.50, there is a continuation of numbers.
While for the square root of 3 or 2, the value is never terminating.
Also in the Pi value, it is written as 3.14159 followed by dots. Recurring means repeated, for 1/3 it is=0.33333. While for the square root of 2, every decimal is not the same value or repeated numbers.
So the definition of irrational numbers includes these two conditions and becomes not rational. These are the expansion for irrational numbers.

A general shape for all types of numbers.
Here is a shape, he started with the Natural numbers, then a new square of Whole numbers after adding the zero.

Then add the negative and call that box Integers. As if moving up a higher degree. Then followed by the rational numbers afterward the irrational numbers, including for instance the negative value(-) of the square root of 8, sqrt(15), and PI. The big box is called the Real number and a symbol was given as capital R.
The expanded form of a whole number.
The next slide image shows the expanded form of a whole number and how we can express any number by a combination of ones, tens, hundreds, thousands, and more based on the value of that number.
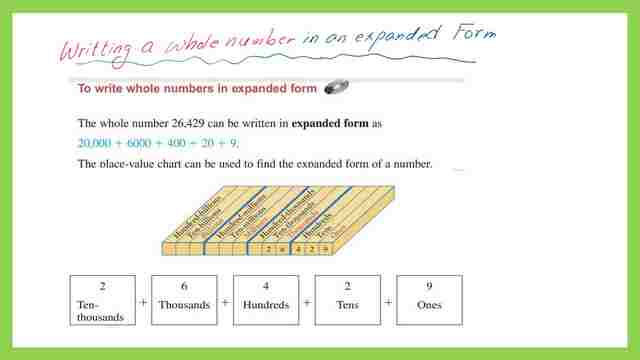
What is rounding of a number?
The rounding subject is one of the important topics. Rounding numbers for instance, if the number is greater than 5, the rounding will increase the number to a higher number. On the contrary, if the number is less than 5, the number will be reduced. So numbers from 1,2,3,4 can be rounded down.
While for number 5,6,7,8,9, the rounding will be rounding up, rounding will be to 10. For example for 27, it is required to round to the nearest 10.
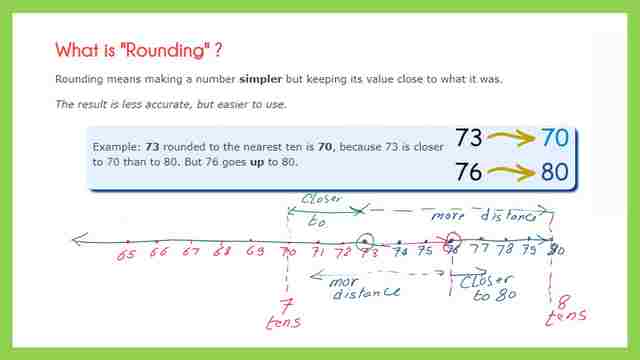
We put a line since the number 7, which is on the right side of the line is more than 5, then round up to 30. While for number=33, put a line at the 3. The 3 at the right of the line is<5 then the rounding of 33 is 30, and it is a round-down.

For Making round to the nearest one hundred and nearest one thousand and beyond. There are examples in the next slide, of God’s will.
Round 4827 to the nearest ten. Since 7>5 then the number at the left of 7 will be upgraded to 3. and 7 will be 0. 7>5. The final number will be 4830. For the same number make a rounding to the nearest hundred. For 4827, put a line at the left of 2, since 2 is <5 then 4827 will be rounded down, then 4827 will be rounded to 4800.

While for 4827 to be rounded to the nearest thousands, take a line between 4 and 8, and check the right side of the line, we have 8 >5, then the number 4827 will be rounded up to 5000 that was for the nearest Thousands We cannot say 4900, since we upgrade 4 to 5.

For an external link, math is fun for the absolute value details.
For the next post, how to round decimal numbers?

