Solved Problems For The Net Area Estimation.
This is an explanation in detail of the content of the subject.
The next slide is a review of the gauge lines showing the first gauge line and the second gauge line in the direction of the force the vertical distance between the gauge lines is g and the distance between the centerlines of bolts is S, which is called the pitch.


The first solved Problem 3-4-2 for the net area estimate of a given angle.
We have two solved problems, the first solved problem 3-4-2, is required to estimate the net area for an unequal angle of 6×41/2″, where 15/16″ holes are used.


For the leg 6″, we have two gauge lines spaced horizontally by s-3″, and g distance =2 1/2″, while g edge distance=2 1/4″.In order to estimate the net area, we make the following steps:
We have to get the gross area from table 1-7 for our angle 6x4x 1/2″ which is Ag=4.75 inch2.
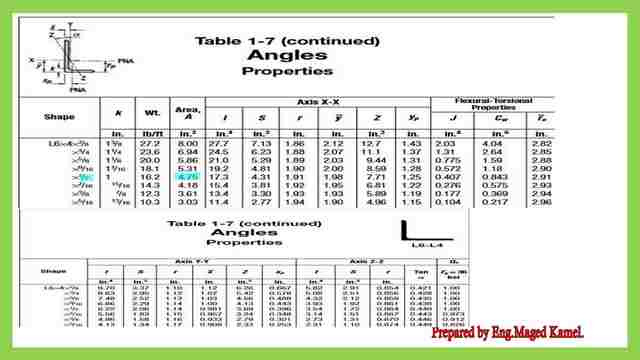

The edge distance g for AB=2.50″, while the g distance for BC =2.25+2.50-(1/4+1/4)=4.25″ since we are deducting the thickness of the angle.
A-check the different path lines and deduct the hole diameter *t, D is 1″ & t=1/2″. The angle is to be unfolded for the evaluation of -g distances based on the centerline distances to the edge as shown in the picture.
For path ac, we have two holes of D=1″, t=1/2″, then Anet=Agross- sum(d*t), Anet= 4.75-2*(1″)*1/2″=3.75 inch2.
B- For path ABB’, we have a zig-zag line Ab, we have to add( t*S^2/4g), where S=3″ and g=2 1/2″, then for the two holes of D=1″, t=1/2″. Anet=Agross- sum(d*t)+S^2/4g, Anet= 4.75-2*(1″)*1/2″+1/2*(3)^2/(4*2.50)=4.20 inch2.


C-check path ABEE’, we have 3 holes of D=1″, t=1/2″, we have two zigzag lines, but each one has different g distances, but with the same S distance.
So we have to add (t*s^2/4*g1)+ (t*s^2/4*g2), then Anet=Agross- sum(d*t)+(t*s^2/4*g1)+ (t*s^2/4*g2).
Anet= 4.75-3*(1″)*1/2″+(1/2*(3^2/(4*2.50)+(1/2*(3^2/(4*4.50)= 4.75-1.5+0.70=3.95 inch2.


D-check path ABCC’, we have 3 holes of D=1″, t=1/2″, and we have two zigzag lines, but each one has different g distances.
But with the same S distance, so we have to add (t*s^2/4*g1)+ (t*s^2/4*g2). Anet=Agross- sum(d*t)+(t*s^2/4*g1)+ (t*s^2/4*g2), Anet= 4.75-3*(1″)*1/2″+(1/2*(3^2/(4*2.50)+(1/2*(3^2/(4*4.50)= 3.96 inch2.


The selected path is path ac for which Anet=3.75 inch2, with the least area for the solved problem 3- 4-2.
A Solved problem 3-5 for the estimate of net area for C channel.
In the Solved problem 3-5, it is required to estimate the net area for a channel C15x 33.90, which has 4 bolts of dia 3/4 inch.
1-The C channel is to be unfolded, We will deduct 2tw thickness for the sum of the external dimensions of the C channel.


2- Get the area of the channel from the relevant table 1-5, Agross=10.00 inch2.
The I shape consists of two thickened portions for the flange with width=tf-tw=3″ and the thickness is equal to 0.65″.
The middle portion is the web with a height of 15 inches and a width equal to 0.40 inches.


I have drawn the elevation of the I shape, which has four gauge lines the distance between the second and the third gauge is given as 9″.The Other gauge distances are to be calculated by subtracting 9 inches from the overall depth and dividing by Two.


A- Examine the route ABCDE, for the solved problem 4-2, we have one zigzag line BC with S=3″ and g=3+2-1*tweb=5-0.40=4.60″. We have a second zigzag line CD with S=3″ and g=9″.
The third zigzag line DE with s=3″ and g=4.60″.3- four holes to be deducted with D=7/8″. Two holes at the flange with flange thickness=0.65″.
While the other two holes are located at the web, where the web thickness=0.40″.
We can estimate the whole area to be deducted as 2*(7/8)*(0.65+0.40)=1.84 inch2.
We can estimate the ( t*S^2/4g) terms for lines BC, CD, and DE for the solved problem 3-5, as follows:
For BC & DE, since they’re identical, the thickness is taken as the average of (0.65)+(0.40), since the two lines pass through the flange and the web of the channel, then the tav=1.05/2=0.525″.
While the CD route passes entirely through the web, for which the thickness is to be taken as t=0.40″.
The final net area is equal to 8.78 inch2.


This is the next post, the Definition of the effective area for tension members.
Chapter 3 – Tension Members– A Beginner’s Guide to Structural Engineering is a great external resource.

