Last Updated on March 24, 2025 by Maged kamel
Moment of inertia Ix for the Trapezium.
1-For the moment of inertia Ix for the trapezium, it can be obtained by considering the trapezium as consisting of one big rectangle, from which two triangles are subtracted, as shown in the following slide.
The Trapezium with base b and the upper top side a and height h, is divided into the following shapes:
1- A rectangle of base b and a height of h, its area A1=b*h, is CG apart from the y-axis by a distance x1= (b1+0.50*a).
2-A left triangle of base b1 and a height of h, its area A2=1/2*b1*h, it is CG is apart from the y-axis by a distance x2=(2/3*b1).
3-A right triangle with a base b2 and a height of h has an area A3=1/2*b2*h. Its CG is apart from the y-axis by a distance x3=(b1+1/3*b1).
The area of the trapezium is the area of the rectangle—the area of the left triangle—and the area of the right triangle.
The details of these shapes are shown in the following slide images.

The value of Ix for the rectangle.-Ix for the rectangle =b*h^3/3.
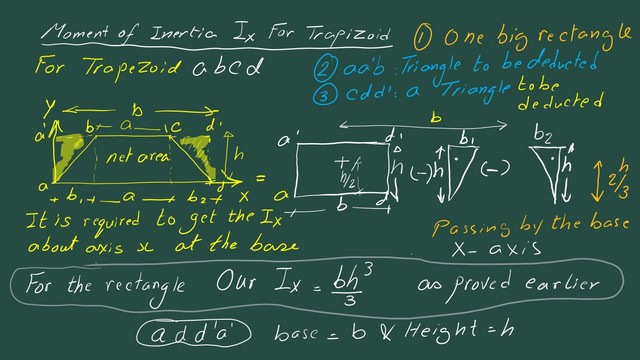
The moment of inertia Ix for the upper left triangle at the x-axis at the base of the trapezium is to be obtained by adding (A*y^2 bar) to the moment of inertia about the Cg for that right-angle triangle, Ixg of that triangle.
The y-bar =(2/3)h, where h is the height of the triangle and the same for a triangle.
Adding the two figures together will give us the final value for triangle 4—the Ix for the upper right triangle at the x-axis, which can be obtained by adding (A*y2 bar) to the Ixg of that triangle. This is the final value of Ix for the triangle at the left edge.

The final Ix value is estimated as Ix for the rectangle -Ix for the left triangle- Ix for the top-right (tr)triangle.
Ix for the trapezium is the ix value for the rectangle minus the sum of inertia for two triangles.

Finally, the Ix for the trapezium can be obtained as the summation of the three inertias. Since we deduct the two inertia values of the two triangles, we put a minus sign.
This is the final value for Ix for the trapezium, where the x-axis passes by the base.

We can convert the trapezium into a triangle by omitting the value a, so we can get the expression for Ix for a triangle, as shown in the next slide. In that case, the final value of Ix for the triangle = h3/12*(b1+b2).
Again, if we consider b1=b2=0, we will get Ix= h3*(3*a+(0+a+0)/12)= a*h3/3, which is the Ix for a rectangle at the base. In the case when a=0, what will be the value of Ix?

Moment of inertia Ix for the trapezium at The CG.
Ix at the trapezium Cg can be obtained using the parallel axes theorem by subtracting(Ay-bar^2) from the Ix of the trapezoid. A is the area of the trapezium, Y bar value=((h/3)(2a+b)/(a+b)).

The next pictures show the step-by-step procedures for getting the final Ix value. The related calculations for ix at the centroid for the trapezium.

We simplify the expression by adjusting similar terms, changing the terms for ix at the Cg for the Trapezium.

Finally, the Ix for the trapezium value at the Cg can be written as shown in the next slide image, together with ix for the trapezium about an x-axis at the base.

The radius of gyration rx for the trapezium at the x-axis.
The square of rx, at an external axis that passes at the base of the trapezium, can be obtained by using the expression of Ix=A*rx^2; we have the area=0.50*(a+b)*h, so we can get the square radius of gyration about the x-axis by dividing Ix/A and trapezium area.
The final expression is shown in the next slide image; the value of rx^2 matches the value in the FE reference handbook.

The radius of gyration rx g for the trapezium at x’-axis passing by the CG.
The radius of gyration rx at the x’-axis passing by the Cg can be obtained by using the expression of Ixcg = A*rxg2. We have the area=0.50*(a+b)*h, so we can get the square of the radius of gyration about the X’-axis passing by the CG by dividing Ixg/A and trapezium. The expression is given in r2x.

The final expression is shown in the next slide image. The value of rxg^2 matches the value shown in the FE reference handbook.

Please refer to post 24 for Ix option 2 for the trapezium. How can I use a horizontal strip to get the Ix value?
Please refer to post 22 for the moment of inertia Iy for the Trapezium.
For practice problems, please refer to posts 25 and 26.
For the use of a calculator for various shapes, please find Moments of Inertia – Reference Table.
This is a link to the complete details of how to get an x-bar and y-bar for a Trapezium.
This is the next post-Ix for a parallelogram.