Ix for the Trapezium second option.
Derive the expression for k1 for the horizontal strip.
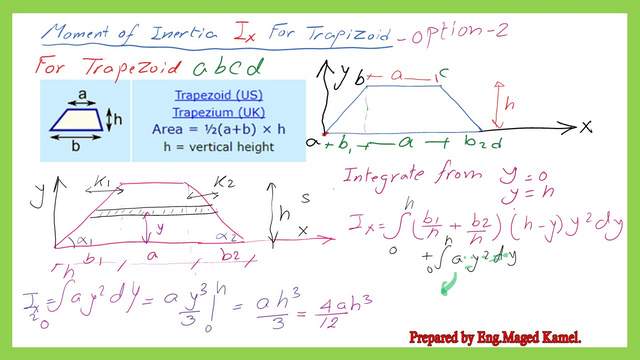
For the Ix for the trapezium second option, we will use a horizontal strip of width dy.
The strip is located at y distance from the Trapezium with a length of (k1+a+k2) where a is the top length of the trapezium.
For a rectangle of base b, we want to get an expression for the value of k1, we consider the left triangle with a base equal to b1 and height equal to h. Using the relation of (k1/b1)=(h-y)/h to get the K1 value. K1 can be written as equals b1*(h-y)/h. Please refer to the next slide image for more details.
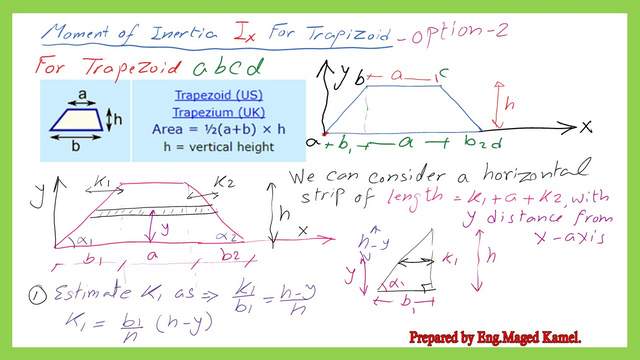

Derive the expression for k2 for the horizontal strip.
Similarly, we want the value of k2, we refer to the right triangle that has a base of b2 and height equals h. Using the relation of (k2/b2)=(h-y)/h to get the k2 value. K2 can be written as equals b2*(h-y)/h. Please refer to the next slide image for more details.
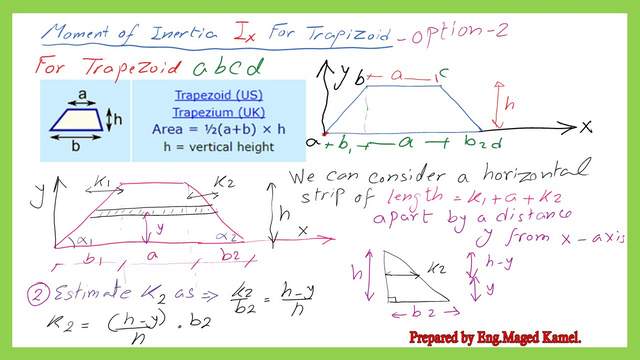

Integrate the horizontal strip.
The moment of inertia Ix for the Trapezium second option can be obtained by integrating the horizontal strip from y=0 to y=h. The length of the horizontal strip can be written as equal to (a+b1+b2)=(a+b1*(h-y)/h+b2*(h-y)/h).
The inertia of the strip dIx=(a+b1*(h-y)/h+b2*(h-y)/h)*y^2*dy
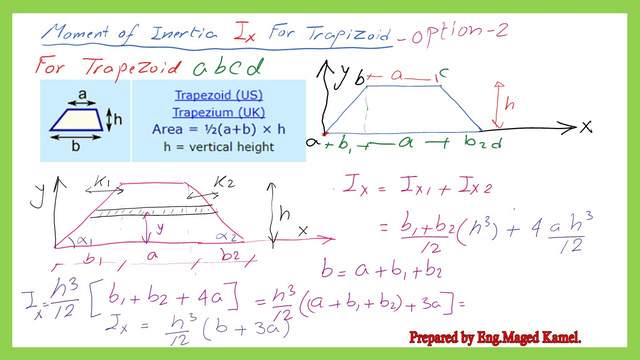
We can simplify the expression as consisting of two items Ix1 plus Ix2
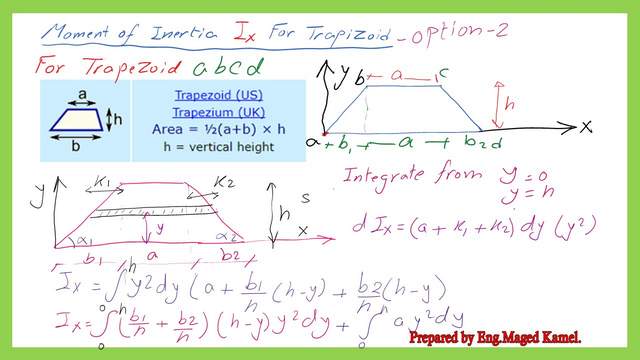

We can simplify the expression as consisting of two items Ix1 plus Ix2. We can clear the common items and get the expression as shown in the next slide image. Ix1 can be written as (b1+b2)*h^3/12.
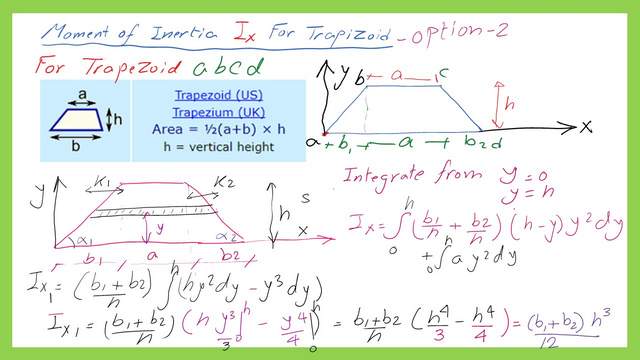

We can clear the common items and get the expression as shown in the next slide image. Ix2 can be written as (4*a*h^3)/12. please refer to the next image for more details.

Derive the final expression for Ix for the Trapezium second option.
We can add the value of ix1 plus Ix2 to get the final expression for Ix for the Trapezium second option.
The Ix value for the trapezium can be expressed as equal to h^3*(b+3a)/12. For the next post, we will solve two practice problems for trapezium. Thank you.

For the use of a calculator for various shapes, please find Moments of Inertia – Reference Table.
This is a link to the complete details of how to get an x-bar and y-bar for a Trapezium.
This is the next post- Two Practice problems for inertia for trapezium.


