Last Updated on September 19, 2023 by Maged kamel
Two Practice problems for polar of inertia for trapezium.
We will introduce two practice problems for the polar of inertia for trapezium which are 8.42, 8.48. these problems are quoted from Engineering mechanics statics by BEDFORD.
The first practice problem for inertia is 8.42. Find Jo and ko for a given trapezium.
For the first practice problem of the two Practice problems for polar of inertia, we have a trapezium of 7 ft base length, and the upper part length is 3 Ft and it is required to determine the moment of inertia ix and the radius of gyration Kx.
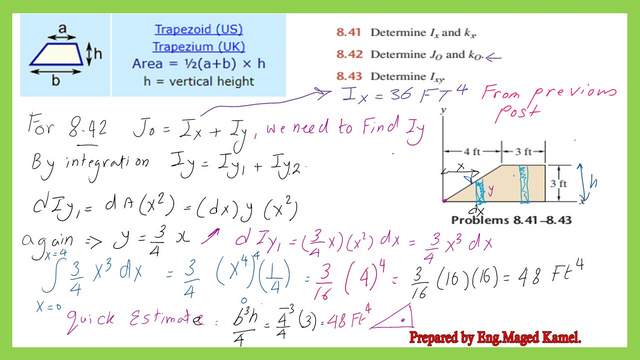
We have already estimated the Ix value of the trapezium from the previous post, the value of Ix equals 36 ft4, please refer to the previous post for more information.
Since Jo=Ix+Iy, we have the value of Ix, we need to estimate Iy or the moment of inertia about the y-axis that passes by the left corner
Iy for a given trapezium by integration using a vertical strip.
As we can from the next slide image we can use a vertical strip of y height and of width equals dx. The inertia of this strip about the Y-axis is the sum of two inertias the first inertia is dIy1 plus dIy2.
To get the value of dIy1, we multiply the area of the strip by the square of its distance x From the y-axis dIy1=y*dx)*X^2.
We can get the equation of the line of the triangle as y=3/4 x, and y for the rectangular part equals h which is 3 feet. dIy1 is equal to (3/4*X^3*dx) . Integrate from x=0 to x=4. We get the value of Iy1=48 Ft4.
i
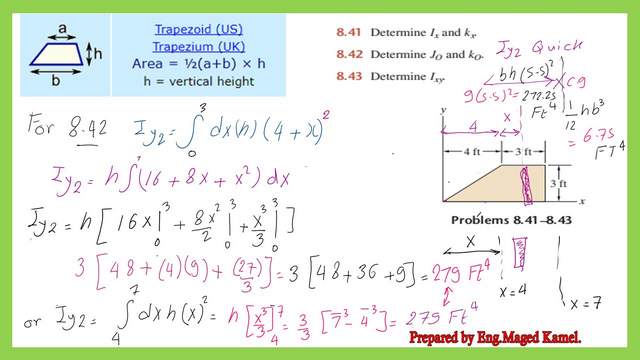
The value of Iy2 for the rectangular portion can be found by integrating the vertical strip from x=4 feet to x=7 feet. The inertia of the strip about the Y-axis for the rectangular portion is equal to the area of the strip multiplied by the square distance from the Y-axis.
Then dIy2=(h*dx*( x+4)^, h value is 3 Ft , and the final value is Iy2 will be found to be equal to 279 Ft4.
The Total Ix value is 36 Ft4. The square of the radius of gyration equals Ix/A=36/15. Then kx equals 1.55 Ft.
The second practice problem for inertia is 8.47. Find Jo and ko for a given trapezium about the Cg.
For the second practice problem 8.47 of the two practice problems the polar of inertia is required to find the moment of inertia for the trapezium at the Cg and also to determine the Ko value. The same Trapezium of 7 ft base length and the upper part length is 3 Ft is dealt with.
Determine the J0 for the Trapezium.
Since the Jo is the sum of ix plus Iy, we have Ix=36Ft4, and the value of Iy final is the sum of Iy1 plus Iy2 which is (48+279)=327 ft4. Jo can be found as the sum of 36 ft4 plus 327 ft4, which is equal to 363 ft4. The next step is to get ko which is the square root of (Jo/A). the area of the trapezium is 15 Ft2. So K0 can be written as equal to sqrt( 363/15)=2.218 ft.
Please refer to the details of the calculations in the next slide image.
Derive a general expression for Iy value.
If you wish to derive a general expression for Iy of the trapezium. The Iy is the sum of Iy1 and Iy2. For Iy1 we can write its expression as equal to the integration from 0 to (b-a) of ((h/b-a)*x^3*dx)) the integration will give a value of (h/4)*(b-a)^3.
While for the integration of Iy2, or the rectangular portion, is the integration from (b-a) to b of (h*dx*x^2), and its final value is ((b^3-(b-a)^3*(h/3)).
Adding Iy1 to Iy2 and after substitution of the values of h, a, and b.Iy= equal to 327 ft4 which is the same as the previously estimated value.
Determine the final expression for Jo for the Trapezium.
Adding the expression for Ix which we have obtained from the previous post, to the general expression for Iy will give us the final expression for jo or the polar moment of inertia for the trapezium.
The final value of jo can be found to be equal to 363 ft4.
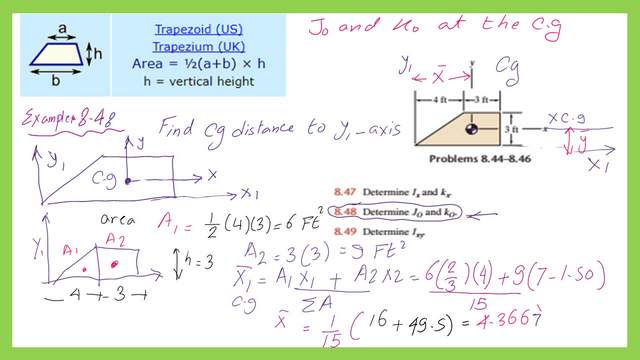
Determine the Jo and ko at the Cg for the Trapezium.
We need to find the x bar of the Cg which is the horizontal distance between the Y axis and the Cg. The x bar can be found from the expression of A(X bar)A1*x1+A2*x2.
Please refer to the next slide image for more detailed information. The x-bar is 4.3667 Ft.
Find the value of Iy at the Cg.
We need to find Iy value at the Cg which is equal to Iy at the external maxis y minus the product of A*X BAR^2.
Iy value is equal to 327 Ft4 and the product of area by the square of x bar is equal to (15*19.06)=285.9 ft4. Iy final value at teh Cg is equal to 40.98 ft4.
To get the final expression for Jo at the Cg, take the square root of (51.63/15)=1.855 ft.
We have to an end after solving the two Practice problems for polar of inertia for trapezium.
Thanks a lot and see you in the next post. Two Practice problems for Ixy for trapezium.
Please refer to post 19 for more information about Ix for a trapezium.
Please refer to post 22 for more information about Iy for a trapezium.
A useful external resource for the area, Cg, and inertia for the parallelogram, please refer to this link.