Area and Cg of a Trapezium.
Reference handbook 10.00 value for area and Cg at the x-direction.
To get the area and Cg for a Trapezium, we will divide the trapezium into a rectangle for which we deduct two triangles and consider taking the first moment of area about a vertical axis y passing by the external edge point about the external axes. This will give the x-bar of the Trapezium.
As for the Y bar, we will do the same process, but the first moment of the area will be taken about an external axis passing by the base which is then called the x-axis.
This is a list of the first moment of area for typical plain shapes. The trapezium data for area and Cg are shown in the fifth shape.


It is required to get the same data as obtained from the FE reference handbook as attached in the next slide image, for case #No.5.
Area and Cg of a Trapezium at the x-direction.
The Trapezium with base b and the upper top side is a and height h, is divided into the following shapes:
1-A rectangle of base b and a height of h, its area A1=b*h, its CG is apart from the y-axis by a distance x1= (b1+0.50*a).
2-A left triangle of base b1 and a height of h, its area A2=1/2*b1*h, its CG is apart from the y-axis by a distance x2=(2/3*b1).
3-A right triangle of base b2 and a height of h, its area A3=1/2*b2*h, its CG is apart from the y-axis by a distance x3=(b1+1/3*b1).
The area of the trapezium is the area of the rectangle-Area of the left triangle- and area of the right triangle, The details of these shapes are shown in the next slide images.


The first moment of areas for these three shapes will be = the first moment of area for the Trapezium.
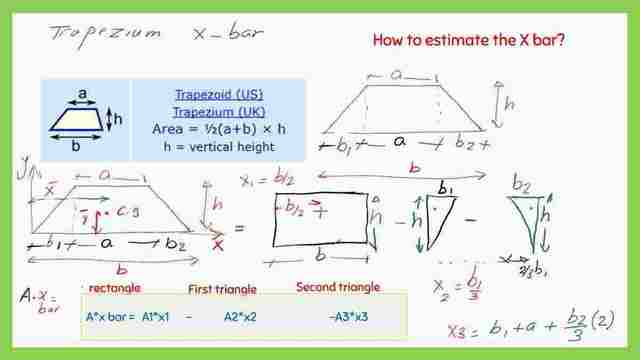

We will proceed with our estimation by equating the first moment of area for the trapezium about the y-axis by the equivalent moments of areas for area A1, A2, A3, (-) minus sign is introduced since we are subtracting areas A2, A3 from A1.


The next two slide images give the full details of the estimation.


Area and Cg of a Trapezium at the x-direction.
We will have the final expression for the distance of the Cg of the trapezium about the y-axis, which is the X-bar.
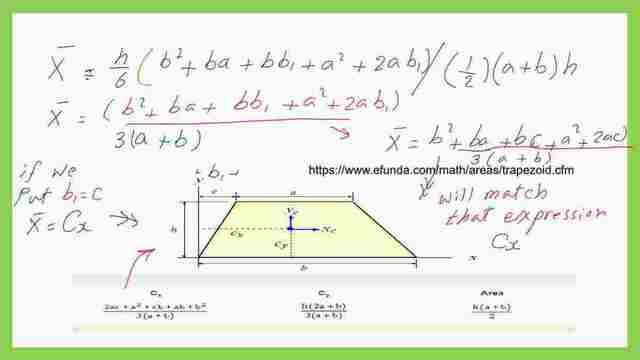

The next link will show the same expression but considered as Cx, I have used b1 in lieu of C. when the Cx value is equal to 1/2*(b-a), where a is the upper side, while b is the lower side, then the Cg distance will be equal to b/2.
Area and Cg of a Trapezium at the y-direction.
The Trapezium with base b and the upper top side is a and height h, is divided into the following shapes:
1-A rectangle of base b and a height of h, its area A1=b*h, it is CG is apart from the x-axis by a distance y1= (1/2*h).
2-A left triangle of base b1 and a height of h, its area A2=1/2*b1*h, it is CG is apart from the y-axis by a distance y2=(2/3*h).
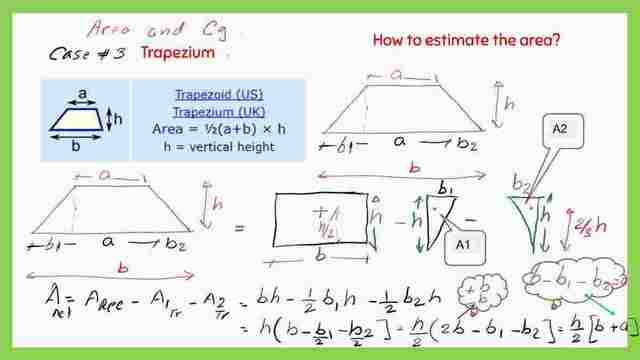

3-A right triangle of base b2 and a height of h, its area A3=1/2*b2*h, it is CG is apart from the x-axis by a distance y3=(2/3*h).
We divide by the area then Y-bar=(1/3)*(2a+b)/(a+b), this result matches the result obtained from the FE reference handbook table of areas and CG.
The final expression of the first moment of area about the x-axis, or A*y bar can be obtained and=(h^2/6)*(2a1+b).
This is a link for the pdf file used in the illustration of this post.
This is a link to review different types of areas and their CG: useful link for areas and Cg.
The second moment of area or the moment of inertia for a Trapezium can be found in post 19.
This is a link for the next post in the area and Cg of a parallelogram.



