The relation between Block shear and coped beams.
Topics included in our discussion are shown in the next slides.
Block shear definition.
We continue discussing the Block shear path graph; the second subject we will discuss is the coped beam and the UBS value condition.
From the site Beginner structural engineering .com / BGSCM14/BGSC. Prof. Thomas Bartlett (Bart) Quimby describes the block shear in the case of the W section, I beam, which is subject to block shear.
There are two modes of failure, the first mode of failure, for which, one part was separated, contains the part of the web, plate, and bolts are included.

The second failure mode involves a T-shaped section consisting of the flange, web, plate, and bolts.
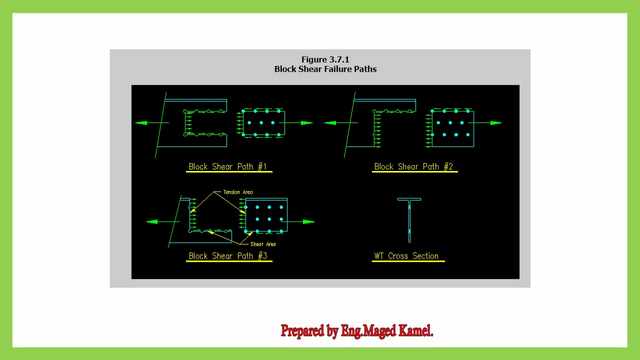
Looking to block shear path no.1, the split section in the middle emerges with the bolts as the tension force acts to the right.
The applied force to the right creates inner forces on the left side, which are tension and shear force.
Because of equilibrium, the tension generated is perpendicular to the left face and acts to the left, whereas the shear force produced is parallel to the force’s direction and acts to the left.
Let us look at block shear path 2. The separated component is in the shape of a T section, which is the tension force, and the faces are parallel to the force direction. However, the shear force created will only affect one face.
Unlike path 1, which has two shear faces, the lower line of bolts is not cut.
The last view is for block shear path no.3, where the cut consists of two lines. The first is vertically up and will create tension force.
The second line, which passes through the bolts, will have a shear force; the sketch to the right depicts the forces in equilibrium. The side view depicts the T portion.
In the block shear strength equation, the nominal strength is 0.60FultAnv, where Anv is the net area for shear, and Ant is the net area for tension plus Ubs*Fult *Ant = <0.60FyAgv+ UBsFuAnt, which is the upper limit.
Using the LRFD, multiply by φ =0.75. To design using the ASD, divide by Ω=2.00. The commentary contains two conditions: the first is for Ubs=1, and the second for Ubs=0.50.

What are the Coped beams?
As illustrated in the sketch, the coped beam is a cut in the secondary beam, which is carried by the main beam.
For the two beams carried by the main beam, a cut is formed for the two flanges on the right and left of the secondary beams, and a connection is produced by using angles bolted to the web of the main beam.
In the second sketch from the right, the beam must be put between two columns using a crane. The cross-section includes both the column and the lateral coped beam.
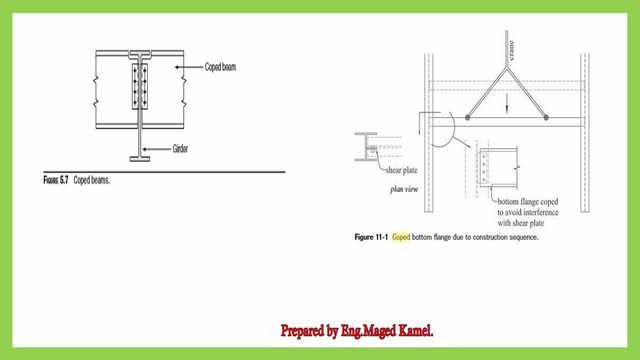
We can see a shear plate. The bottom flange coped to avoid interference with a shear plate. A cut is made to the bottom flange to facilitate crane handling of the beam.
From the next slide, In some cases, field conditions May dictate the requirement of a cope, for example, the previous Figure 11-1, shows a beam framing into the web of the column.
When erecting this beam to its final position, it is dropped down between the Column flanges.
This particular Beam would require a coped bottom flange to be placed without obstruction, so the bottom flange is cut.
Other common coped beam connections are shown in Figure 11-2. In the first figure, a secondary beam rests on the main beam, and the reaction develops due to loading.
The cut is made to support the secondary beam on the top of the flange of the main beam, so a part of both the web and flange was cut,
let us examine the forces the section needs reinforcement to increase the the bending section modulus of the beam to increase Sx.
After the cut of the section, it is reduced into a T section, as shown above, so the reinforcement needed is done by using two plates at each side of the web of the T section.
In the next section, in part b, the top flange cope, where the cut is made in the flange, and includes an angle to connect the secondary beam to the main beam, where the cut is only done for the top flange.
In the next sketch, part c, the cut is done for the upper and lower flanges of the secondary beam, coped at both flanges. The section of the beam is large due to a large reaction, so plenty of bolts are to be used.
The code specifies different shapes with different names.
A beam cope is defined as the removal part of the beam web and flange; here, a cut is made for both the flange and the web.
In the second section, the name block is given due to the removal of small parts of the flange only, so the web was not cut.
A cut is the removal of the side of part of the flange. All shapes can be considered as coped beams.

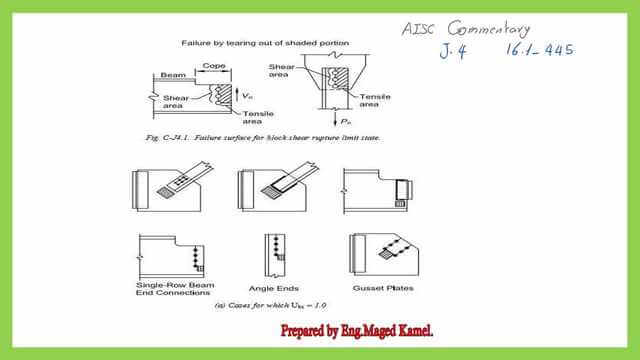
Cases where UBS=1
From the AISC commentary, these are the cases for the UBS value =1.
The new case is tension and shear due to the reaction that pushes, thus creating shear stress in the group of bolts, which are in the vertical direction.
Tension is developed due to the resistance of the tensile area, and the shear area close to the edge has a uniform stress distribution.
The second sketch is for the hanger connected to the gusset plate and here there is a diagonal member in a truss, the member is under tension force, so one face has shear stress and the other faces have shear stress, and other faces have Tension stress.
The other section is for the same connection, inclined member to a gusset plate, but welded.
The last case is the coped beam, which is welded. This sketch is for single-row beam end conditions, and this sketch is for angle ends under tension. Here, we have a gusset plate.
For all these cases, the UBS =1.
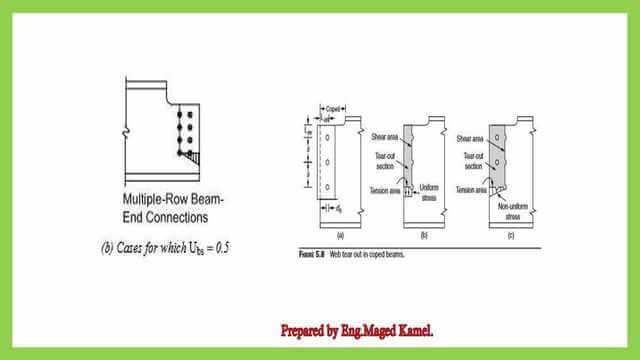
Cases where UBS=0.50
For the cases where the UBS=0.50, for the coped beam.
In case b, Multiple-Row beam-end conditions, the block shear occurs for two lines of bolts, and the tension area will have a triangular distribution of stresses; these stresses are not uniformly distributed.
For the middle part b, the web is torn out in a coped beam; because we have only one line of bolts, there is a uniform tension distribution of stresses.
In the case of C, we have a shear area and tension area with a non-uniform stress distribution; these cases for UBS =0.50.
The related posts are included in The steel beams sections.
The next posts are- post 19- Solution for Block Shear-Coped Beam Problem.
The next posts are post 20—Aisc Tables 9-3a,b, and C for the Block shear-coped beam.
The next posts are- post 21- Case 2 for block Shear-Coped Beam Problem.
There is a very useful external link: Block Shear Rupture, Chapter 3, Tension Members, Beginner’s Guide to the Steel Construction Manual, 14th ed.
This is the next post 14: Solved problem 5-7 for block shear.
