A Solved problem 5-7 for block shear.
Brief content Content of the video.
We continue with A Solved example 5-7 for block shear from Prof. Alan Williams’s book, structural steel design LRFD- ASD. The bolted connection of a tension member to a gusset plate.
For the first sketch a, there are two lines of bolts, the horizontal distance =g, and the vertical distance is is=S, the distance between the first bolt to the left edge = leh.
The right edge is the same=Leh. the vertical distance Lev from the first bolt to the upper edge, and lev to the edge of the gusset plate, then a discussion of the possible block shear for the various failure paths are made.
For the first failure path, if the hatched area was separated, then for the remaining part, there is possible shear stress along the vertical lines of bolts and a tension area for the lower bottom. and for the second pattern two hatched areas.
If separated, the remaining shape will have this irregular shape, and the holes left after splitting, for the third pattern, the gusset plate can have a failure. This video has a subtitle and closed caption in English.
A Solved problem 5-7 for Block shear.
Topics included in our discussion are shown in the next slides. This is a list of the Block shear Equations by the code provision J4-5.
The provision is used to calculate the block shear strength for any plane.
Introduction to the solved problem 5-7 for block shear of tension member connected to a gusset plate through bolted connections, the types of modes of failures are shown from mode b to mode d.
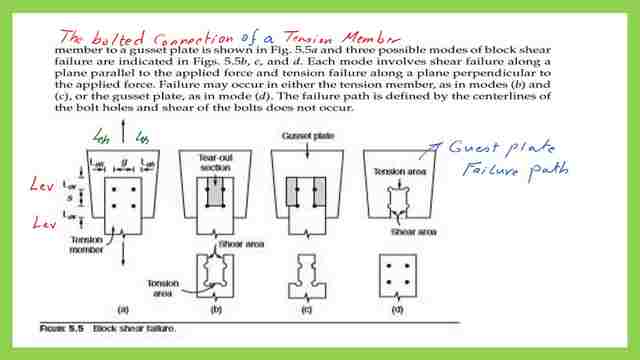
Example 5-7, from prof. Alan Williams’s book, for the tension member connected to a guest plate, the thickness of the tension member is 1/2 inch, while the thickness of the gusset plate is 1″.
It is required to determine the block shear capacity for that hanging rod. The steps are as follows:
1-The diameter for each bolt D will be=7/8+1/8=1″, we add 1/8″ to compensate for both drilling and occurring damage.
2-g, the gauge distance, which is perpendicular to the tension load, here is the horizontal distance=2″ as given, while, s, the pitch distance in the direction of the load=3″.
A Solved problem 5-7 for block shear, an inspection of mode b.
3-We have one plane subjected to tension and two planes subjected to shear.
4- the net area for tension Ant=Agross-2*halves of bolts*t plate, so=Ant=2*1/2-(2*1/2*1/2)=1/2 inch2, while Agt=Agross=2*1/2=1 inch2.
5- for the two areas subjected to shear, we have Agv=2*(5)*1/2=5 inch2, for Anv, we have to deduct 2 dimeters +2 1/2 diameters=3 inch.
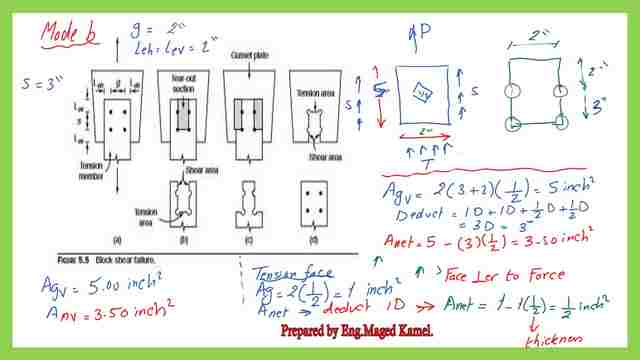
6- the gross area for shear Agv=2*5*1/2=5 inch2, Anv=5-(3*1*1/2)=3.50 inch2.
Fu=58 ksi, fy=36 ksi, Anv=3.50 inch2, UBs=1.0, Ant=1/2 inch2. For the LHS we have the nominal load equal to 0.6*58*3.50+1*58*0.50=150.8 kips.
While for the RHS, we have: the nominal load equal to (0.60*36*5+1.0*58*0.50=137.0 kips, for Rn it is the minimum value of(150.80,137)=137.0 kips.
A Solved problem 5-7 for block shear, an inspection of mode c.
We continue with the solved problem 5-7 for block shear. We have two planes subjected to tension and two planes subjected to shear.
If we consider one plane, then we multiply later on by 2, the net area for tension Ant=Agross-1*half of the bolts*t plate.
Ant=2*1/2-(1*1/2*1/2)=1-1/4=0.75 inch2, then finally Ant=2*0.75=1.50 inch2, while Agt=Agross=2*1/2*2=2 inch2.
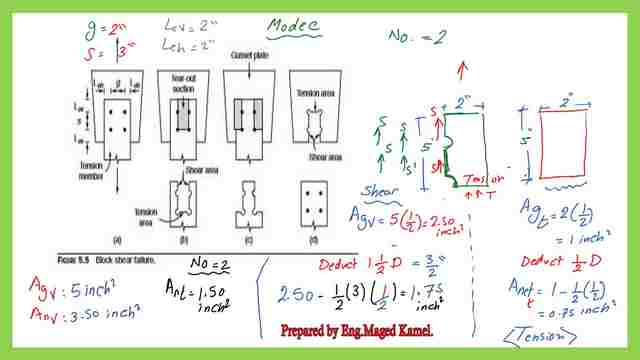
For the two areas subjected to shear, we have Agv=2*((5)*1/2)=5 inch2, for Anv, we have to deduct 2 dimeters +2 1/2 diameters=3 diameters=5-(3*1*1/2)=3.50 inch. Agv=5 inch2, Anv=3.50 inch2. This is the equation for which we will substitute for mode C.
Fu=58 ksi, fy=36 ksi, Anv=3.50 inch2, UBs=1.0, Ant=1.50 inch2. The gross area for shear Agv=5.0 inch2, while the net area for shear Anv=3.50 inch2.
For the LHS=0.6*58*3.50+1*58*1.50=208.80 kips, while the RHS=0.60*36*5+1*58*1.50=195.0 kips, for Rn it is the minimum value of(208.80,195.0)=195.0 kips.
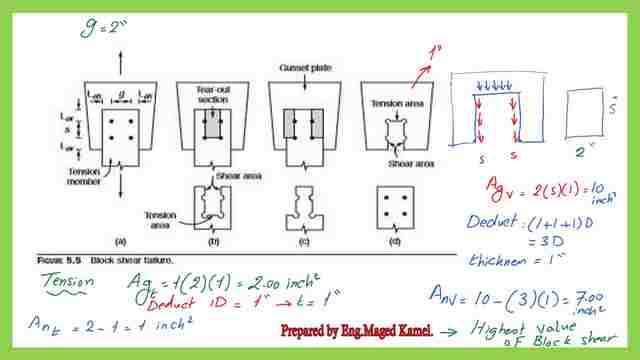
Solved problem 5-7 for block shear, and an inspection of mode d.
We continue with the solved problem 5-7 for block shear, we have one plane which is subjected to tension and two planes subjected to shear, in the gusset plate with 1″ thick.
The net area for tension Ant=Agross-2*half of bolts*t plate, so=Ant=2*1-(2*1/2*1)=2-1=1 inch2, then finally Agt=2.0 inch2, while Ant=1 inch2.
For the two areas subjected to shear, we have Agv=2*((5)*1)=10 inch2, for Anv, we have to deduct 3 dimeters Anv=10-(3*1*1)=7.0 inch. The Agv=10 inch2, while Anv=7 inch2.
Since these values are very high as compared to the two previous modes b&c, we will not proceed to estimate the Rn value.
The final answer will indicate that failure will occur first based on mode b since it gives the smallest Rn out of the three failure modes b,c,d, which is 137.0 kips, while for mode c Rn=195.0 kips.
Again for the LRFD, we will multiply by Phi=0.75, Φ*Rn=0.75*137=102.75 kips for the LRFD, while for the ASD, we have Ω=2.0 then 1/Ω*Rn=(1/2)*137.0=68.50 kips.
This is the PDF used in the illustration of this post.
This is the previous post#13, The relation between Block shear and coped beams. Please refer to this link.
The next post is problem 3-7 for staggered bolts.
For a more detailed illustration of block shear, there is a very useful external link-Block Shear Rupture. A Beginner’s Guide to the Steel Construction Manual, 14th ed.
