Last Updated on June 7, 2024 by Maged kamel
Solved problem 10-1 for the Design Of Steel Section For Continuous Beam-Part-4/4.
The negative moments are due to dead uniform loads and concentrated loads.
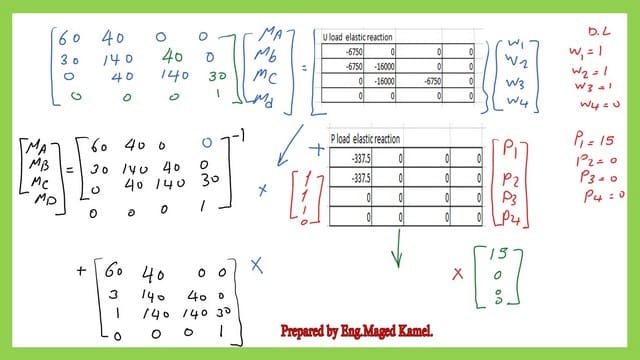
We will substitute the values of spans and loads; the general form of the matrix, as we have done, enables us to use it to get the values of the bending moments for different span lengths and different loading values.
The values of span lengths are for the first span length L1=30′, for the second span length L2=40′, and for the third span length L3=30′.
We will substitute in the first matrix, as 2*L1=60, L2=40′, L1=30′ 2*(L1+L2)=2*(30+40)2*70=140′, 2*(L21+L3)=2*(40+30)2*70=140′, we will put the zeros where it is located in the matrix.
As for the elastic reactions matrix for the uniform loads vector matrix, we have -L1^3/4=-(30^3/4)& -L2^3/4=-(40)^3/4 &-L3^3/4=-*(30)^3/4.
As for the elastic reactions matrix for the concentrated load’s vector matrix, we have only one parameter, which is -(3/8)*L1^2=-(3/8)*(30)^2, which we will substitute in the next slide. These values are shown for the matrix 4×4, the vector matrix for moments (MA MB MC MD).
I have used an Excel sheet to solve the problem, and these are the values for the elastic reaction parameters for the vector matrix for uniform loads. These are the original parameters as shown, -L1^3/4=-(30)^3/4=-6750& -L2^3/4=-(40)^3/4=-16000& -L3^3/4=-(30)^3/4=-6750.
We need to estimate the inverse of the matrix to solve for the negative moments. We can get the inverse value of the matrix by using Excel or other programs, and the matrix inverse is denoted by the symbol -1.
When multiplying by the inverse matrix on the left-hand side, we get the unity matrix, where the diagonal is 1, and all other elements are zeros.
We will multiply the inverse of the matrix by the elastic reaction parameters, again by the concentrated load’s column-vector matrix. Where P1=15 kips, P2=P3=P4=0, the vector column matrix is( 15 0 0 0). We have the vector column matrix on the left-hand side (MA MB MC MD) and two matrices added together.
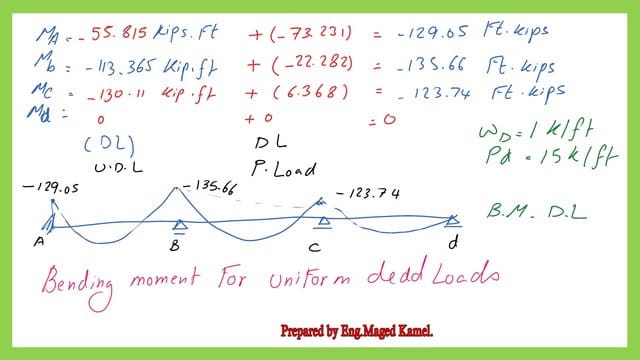
The next slide shows the bending moment values for dead loads.
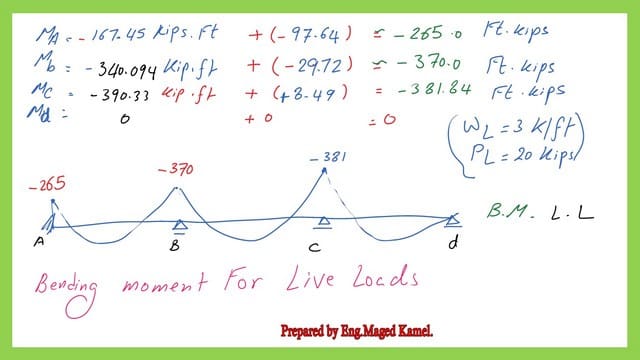
The next slide shows the bending moment values for Live loads.
The Bending moment for the Total service loads.
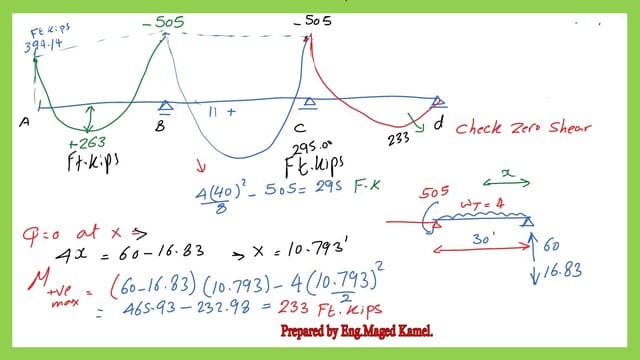
We add the negative bending moments due to dead and live moments to get the negative values for each support. The moment at support A, MA=-394.14 Ft.kips. The moment at support B, MB=-505.0 Ft.kips. For the positive bending moments.
The moment at support c, Mc=-505.0 Ft.kips. For the positive bending moments. There is no negative moment for the end support D, so Md=0.
The next slide image shows the positive values for spans AB, Bc, and Cd.
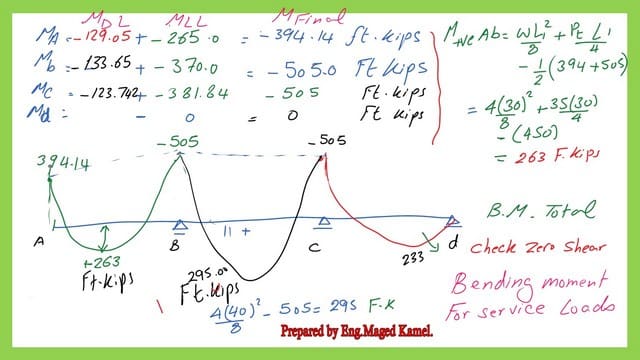
In the next slide, we will check that the shear value at the end span CD is zero for the point of maximum positive moment. The maximum moment value is 233.0 Ft.kips.
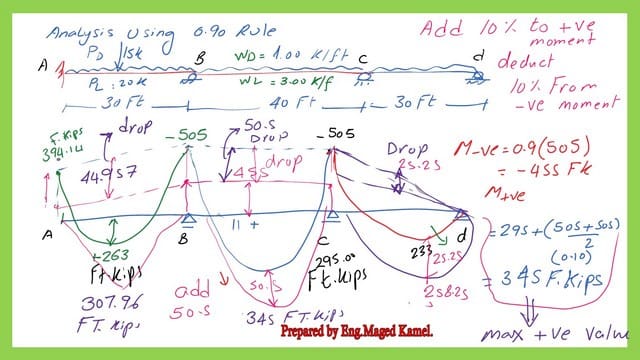
The elastic redistribution for a moment or 0.90 rule.
For the maximum positive value of Moment, we have span AB with M+ve=+263.0 Ft.kips, span BC with M+ve=+295.0 Ft.kips, and span CD with M+ve=+233.00 Ft.kips. The largest value is +295.0 Ft.kips, so we add the 0.10*average of (505.0).
The moment diagram shows that the maximum negative moment equals 505 Feet, while the maximum positive moment is 295.0 feet. These values are before using the 0.90 rule.
for the 10% reduction of the negative moment at span BC , we multiply 0.1*(505), and we get 50.50; the final value of the negative moments at supports B and C will be -+-455 ft. kips. We add the drop to the positive value of moment at span BC; the final value will be equal to (50.50+295)=345 Ft.kips.
For the added values for the edge supports, we add 10% of the average negative moments, as shown in the next slide image.
Design of steel section for continuous beam based on the maximum moment.
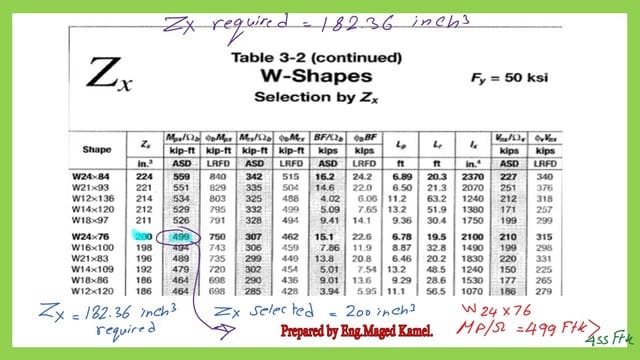
We have two maximum values, one for a maximum positive moment, which is 345 Ft. kips, while the other value is for the maximum negative moment, which is -455 Ft.kips. We check the bigger value of 455 Ft.kips. We estimate the Nominal moment, we divide 455 by omega,1.67. The nominal moment equals 760 Ft.kips. We use Table 3.2, to select the appropriate lightest W section. For the steel section for continuous beam, Zx required 182.36 inch3.

The selected W section is W24x76 and has Zx=200.0 inch3. The Zx value is bigger than the required Zx. This is the Final check for the design of the steel section for continuous beam 3-3.
This is a link to the previous post part 3-4.
Have more information about the structural analysis –III.
For more details about the upper bound and lower bound

