Solved problems for 3×3 matrix by Crout’s LU-option -1.
We have two solved problems for the 3×3 matrix by Crout’s LU decomposition. for which we will apply the same technique used to derive the elements of the lower matrix and the upper matrix.
The first solved problem for the 3×3 matrix by Crout’s LU-Option-1.
The first problem for the 3×3 matrix is Crout’s LU decomposition. It is required to find both the Lower and upper matrix decomposition LU by using Crout’s method through a given matrix A. The given matrix is 3×3.
We will apply the previous post technique to get the L1 and U1 matrix components by using the following steps.
Step-1 Convert matrix A to a lower matrix.
First, we have matrix A as (1 1 1, 4 3 -1, 3 5 3 ). We will estimate the determinant value of this matrix A, it is estimated as equal to +10. Since the determinant value is not equal to zero, then the matrix is invertible and we can proceed to find L and U matrices based on Crout’s method.
The three elements in the first column vector of the A matrix which are 1 4 3 will be set as L11 &L21 and L31. L11=1, L21=4,L31=3. While for U12, we will divide a21/a11=1/1=1. While U13=a13/a11=1.
As for the upper matrix U1, the u11=1, U12=a21/a11=1/1=1 and u13=a13/a11=1/1=1. The detailed procedures are shown in the slide image.


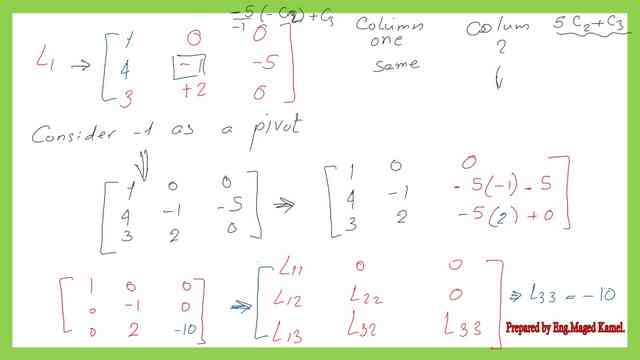
Step-2-Derive the values for the L22, L23, and U23-option-1.
We will use a11 as a pivot, we multiply (-1)*(a12/a11)*column 1 and add the result to the 2nd column, similarly, we multiply (-1)*(a13/a11)*column 1 and add the result to the 3rd column. If we call the new matrix L1, the elements of the matrix are as follows:
The first row is (1 0 0). The second row is (4 -1 -5). The third row is (3 2 0). If we compare the first row of L1 to the next matrix, we have (L11 0 0), then L11=1. If we compare the second row of L1 to the next matrix, we have (L21 L22 L22*U23), then L21=4.
If we compare the third row of L1 to the next matrix, we have (L31 L32 L32*U23+L33), then L31=3 and L32 =2.


Step-3-Derive the value for the L33.
We want to proceed to get the final l matrix, we want to let -5 equal zero. We multiply (-1)*(-5/-1)*column 2 and add the result to the 3rd column. The final elements of the Lower matrix l will be as follows:
The first row is (1 0 0). The second row is ( 4 -1 -5*-1+(-5)). The third row is ( 3 2 -5*2+(0)).

Step-4-Check the product of(L*U)=A-matrix for a 3×3 matrix.
In the final slide, we have all the elements in the first column of the matrix identical to the first column of the lower matrix. The diagonals of the U matrix U11=U22=U33=1. L22=-1. U23=+5 while L33=-10. U12=1 and u13=1.
We can write both the lower matrix and the upper matrix and check whether the multiplication of the lower matrix by the upper matrix will give us the final A matrix or not. Using the row-by-column multiplication, we can see that L*U multiplication will give the matrix A.


The second solved problem-Crout’s LU-Option-1.
First, we have matrix A as ( 10 3 4, 2 – 10 3, 3 2 -10 ). We will estimate the determinant value of this matrix A, which is estimated as equal to +1163 Since the determinant value is not equal to zero, then the matrix is invertible and we can proceed to find L and U matrices based on Crout’s method. The second solved problem, the detailed procedure to estimate the determinant is shown in the next slide image.


Step-1 Convert matrix A to a lower matrix.
The three elements in the first column vector of the A matrix which are 10 2 3 will be set as L11 &L21 and L31. L11=10, L21=2,L31=3. While for U12, we will divide a21/a11=3/10=3/10. While U13=a13/a11=4/10.


Step-2-Derive the values for the L22, L23, and U23.
We will use a11 as a pivot, we multiply (-1)*(a12/a11)*column 1 and add the result to the 2nd column, similarly, we multiply (-1)*(a13/a11)*column 1 and add the result to the 3rd column. If we call the new matrix L1, the elements of the matrix are as follows:
The first row is (10 3 4). The second row is (2 -10 3). The third row is (3 2 -10). If we compare the first row of L1 to the next matrix, we have (L11 0 0), then L11=1. If we compare the second row of L1 to the next matrix, we have (L21 L22 L22*U23), then L21=2.
If we compare the third row of L1 to the next matrix, we have (L31 L32 L32*U23+L33), then L31=3 and L32 =.1. To get U23 divide ((2.2)/(-10.6)=-11/53.
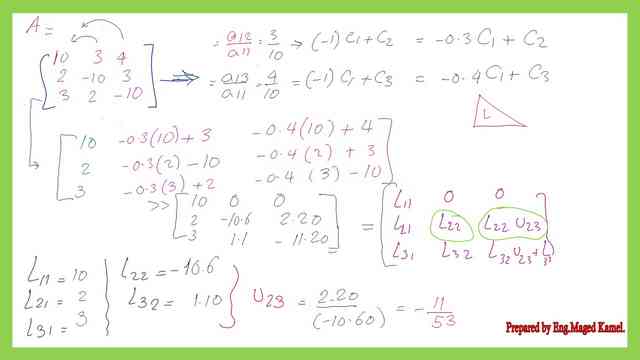
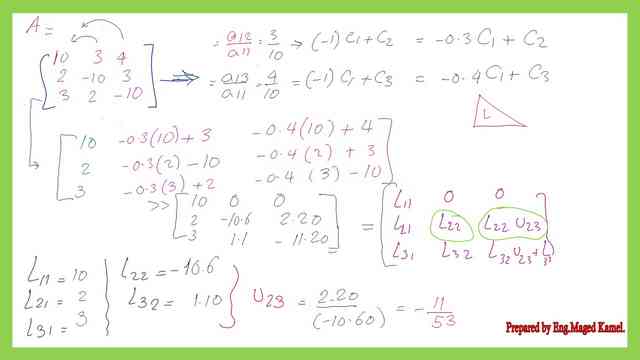
Step-3-Derive the value for the L33-Crout’s LU decomposition.
We want to proceed to get the final l matrix, we want to let 2.2 to be equal zero. We multiply (-1)*(2.2/-10.60)*column 2 and add the result to the 3rd column. The final elements of the Lower matrix l will be as follows:
The first row is (10 0 0). The second row is ( 2 -10.60 0). The third row is ( 3 1.1 -1163/106). As we can see L33 will be equal to -1163/106.


Step-4-Check the product of(L*U)=A-matrix for a 3×3 matrix.
Using the row-by-column multiplication, we can see that L*U multiplication will give the matrix A.


The full detailed steps are shown in the previous slide images, at the end we will check the product of L*U against the Matrix A value.
This is a link to the next post is the introduction to the permutation matrix.
References
This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.
Another calculator to use is a Calculator for matrices.

