Last Updated on May 23, 2023 by Maged kamel

A Second option for Crout’s LU decomposition-3×3 matrix.

In this post, we will discuss how to get the elements of the lower and upper matrices using Crout’s method for the 3×3 Matrix.

 We have two options; the second option is to convert matrix A to an upper matrix, then we can get all the elements of the upper  Matrix, and besides, we can get the value of L22&L32 and L33.

The details of equating Matrix A to the multiplication of the lower Matrix L by the upper Matrix U are shown on the slide page

Step-1-equate the product of L*U to the A- matrix.

We have three equations for which we want to develop Crout’s LU decomposition for a 3×3 matrix.
The first equation is (a11*x1+a12*x2+a13*x3=b1). The second equation is (a21*x1+a22*x2+a23*x3=b2).

The third equation is (a31*x1+a32x2+a33*x3=b3).

We can express these equations as A*x=b. The next task is to try to get L and U matrices using Crout’s LU decomposition for a 3×3 matrix-Option 2.

The matrix A which is(a11 a12 a13,a21 a22 a23, a31 a32 a33). Consider the lower matrix L matrix as (L11 0 0, L21 L22,0, L31 L32 L33) which is a 3×3 matrix.

Using the expression of L*U =A, we can drive a new matrix which is a 3×3 matrix, that contains the elements of both the lower and upper matrix.

 If we write  A as  3×3, for which the elements are (  a11  a12 a13, a21  a22  a23, and  (a31 a32 a33) equal to the multiplication of L by U.

We know that according to Crout’s method, we have all the diagonals of Matrix U are Ones. The left-hand side is Matrix A, while on the right-hand side are L*U matrices.

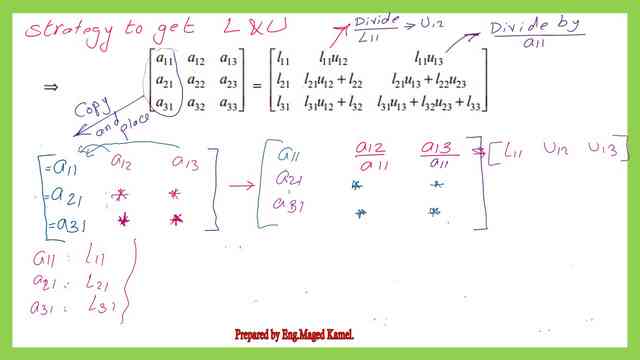
Step-2-Derive the expression for L11, L12, L13 & U12, U13.

The second slide shows that the three elements L11&L21 and L31 are equal to a11&aa12 and a13. While a1U12=a21/L11 and since L11 equals a11, we can derive the expression of u12 as equal to (a12/a11), and similarly, U13 is equal to a13/a11.

As a quick reminder of the values of L11, L21, and L31, Copy the entire first column of matrix A and place it in the first column of the Lower matrix. Divide a12/a11 this is the value of U12 and Divide a13/a11 this is the value of U13. Please refer to the next slide image.

Step-3-A Second option for Crout’s LU decomposition-3×3 matrix.

Option 2 is to convert matrix A to an upper matrix, as shown in the slide. We want a21 and a31 to be zeros; we set a11 as a pivot, then multiply the first row by (-a21/a11) and add the result to the second row.

. The new matrix if we call it A1, has the first column as (a11 0 0), the second column elements are (a12 ((a22-a21/a11*(a12)) (( a32 -a21/a11*(a12)). The third column elements are (a13 ((a23-a21/a11*(a13)) (( a32 -a21/a11*(a12)). For the third row/ third column, the element will be set equal to L31U13+L32U23-U13L31+L33=L23U23+L33.

Step-4- How to find L22, and L32?

If we look at the second row / second column element of matrix A, we have (a22=L21*U12+L22), so we can get a value for L22 equal to (a22-L21*U12) or l22=a22-a21*a12/a11.

While the third row / second column element of matrix A is a32,  we have (a32=L31*U12+L32), so we can get a value for L32 equal to (a32-L31*U12) or L32=a32-a31*a12/a11.

If we refer back to matrix A1, we find that the second row /the second column, which is ((a22-a21/a11*(a12)) can be set equal to L21.

The third row/ the second column, ((a23-a21/a11*(a13), can be equal to L32. If we refer back to matrix A1, we find that the second row /the third column, which is (( a32 -a21/a11*(a12)), can be set equal to L22*U23.

The third row/the third column, (( a32 -a21/a11*(a12)) can be equal to L32*U23+L33.

Step-5- How to find L33, U23& U12, and U13?

We move to the next slide and check the final terms of matrix A, from which we can get the values of L22 and L32. We proceed to get
matrix U1 by letting L32=0. We use L22 as a pivot, multiply the second row by(-1)*L32/L22 and add the value to the third row.

The Final upper Matrix contains the following: As a first row, we have (L11 U12*L11 U13*L11); as a second row, we have (0 L22   L22*U23 ); as a third row, we have (0 0 L33).

To get the values of U12 and U13 divide the first row/second column element by L11 and divide the first row/third column element by L11. To get U23 divide the second row/3rd column element by L22. A summary of the steps we made to Get L22 and l23 elements.

A summary of the steps we made to Get L33 &U12 and U13.

This is a link to download the PDF file used for the illustration of this post.

The next post is Solved problems for 3×3 matrix by Crout’s LU-option 1.

This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.

This is a link to another –Calculator for matrices.