9- Crout’s LU decomposition for a 3×3 matrix-Option 1

Crout’s LU decomposition for a 3×3 matrix-Option 1.

The elements of the upper and lower matrix, 3×3, can be obtained by using the Gauss elimination method. The U matrix for Crout’s LU decomposition for a 3×3 matrix is (3×3) matrix composed of (u11 u21 u13) or the first row, and ( 0 1 u23) for the second row. For the last row, the matrix is (0 0 1).

The process of finding the components of both the lower L and the upper U matrix is explained in the following steps.

Step-1-equate the product of L*U to the A- matrix

We have three equations for which we want to develop Crout’s LU decomposition for a 3×3 matrix.
The first equation is (a11*x1+a12*x2+a13*x3=b1). The second equation is (a21*x1+a22*x2+a23*x3=b2).

The third equation is (a31*x1+a32x2+a33*x3=b3). We can express these equations as A*x=b. the next task is to try to get L and U matrices using Crout’s LU decomposition for a 3×3 matrix Option 1.

The matrix A which is(a11 a12 a13,a21 a22 a23, a31 a32 a33). Consider the lower matrix L matrix as (L11 0 0, L21 L22,0, L31 L32 L33) which is a 3×3 matrix.

Using the expression of L*U =A, we can drive a new matrix which is a 3×3 matrix, that contains the elements of both the lower and upper matrix.

By writing down the matrix A as  3×3 (a11  a12 a13, a21  a22  a23 and  (a31 a32 a33) =the multiplication of l by U, or the multiplication of ( L11 0  0, L21 L22  0, L31 L32  0) multiplied by  ( 1 U12 U13, 0  1  U23, 0  0 1), as we know that according to Crout’s method, we have the diagonal of Matrix U is ones. The left-hand side is matrix A, while on the right-hand side are L*U matrices.

Step-2-Derive the expression for L11, L12, L13 &U12, U13 for Crout’s LU decomposition for a 3×3 matrix.

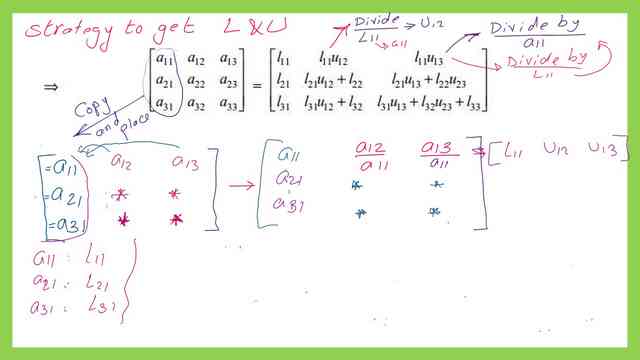
From the second slide, we can see that by multiplying the first row of the lower matrix by the First Column of the upper matrix, we get (L11*1)  equal to the first element a11 of matrix A.

Multiply the third row of the lower matrix by the First Column of the upper matrix, we get (L31) which will be equal to a31.

At first sight, we see that the first column of The lower triangulation matrix is identical to the first column of the original Matrix, since L11=a11. L21=a21, L31=a31.

We will proceed to multiply the first row of the lower matrix by the second column of the upper matrix. We can write that (l11*u12 +0*1+0*0)=a12.

We have L11 equals to a11, so U12 will be set=a12/a11, since L11*U12=a12.

If we multiply the first row of the lower matrix by the third column of the upper matrix. We can write that (l11*u13 =a13. So U13 will be set=a12/a13, since L11*U13=a13. We have L11 equals to a11, so U12 will be set=a12/a11, since L11*U12=a12.

As a quick reminder of the values of L11, L21, and L31, please Copy the entire first column of matrix A and place it in the first column of the Lower matrix. Divide a12/a11 this is the value of U12 and Divide a13/a11 this is the value of U13. Please refer to the next slide image.

.

Step-3-Convert A matrix to a lower matrix as option-1-Crout’s LU decomposition for a 3×3 matrix.

Option 1 is to convert matrix A to a lower matrix, as we can see from the slide. We want a12 and a13 to be zeros, we set a11 as a pivot, then multiply the first column by (-a12/a11) and add the result to the second column. Similarly, we can multiply the first column by (-a13/a11) and add the result to the third column.

If we have a look at the second row / second column element, we have (a22-a21/a11*a21). Please refer to the upper left corner of this slide, if we compare matrix A and the product of l by U, we can see that a22=L21*U12+L22.

Since we know already that a21/a11=U12, L21=a12.So we can rewrite the second row / second column element, which has (a22-a12/a11*a21) to be equal to l21*u12+l22-U12*L21=L22. So we can rewrite the third row / second column element, which has (a32-a12/a11*a31) to be equal to L31*u12+l32-U12L31=L32.

For the second row/ third column, the element will be set equal to L21*U13+L22*U23-U13*L21=L22*U23. For the third row/ third column, the element will be set equal to L31*U13+L32*U23-U13*L31+L33=L23*U23+L33.

Step-4-Derive the value for the U23 for Crout’s LU decomposition for a 3×3 matrix.

After adjusting its rows, we move to the next slide and check the lower matrix L1.

We can get the value of U23 by dividing the 2nd row/ 3rd column element over the second row/second column element. We want to let L22 U23 equal zero to reach the final lower matrix L.

Consider L22 as a pivot. Divide L22*U23/L22, multiply by (-1) *second column, and add the result to the third column.

Step-5-The final Crout’s LU decomposition for a 3×3 matrix.

We will move to the last slide, as a summary from matrix L1 we can get the value of U23 as we have explained.  The final L matrix will give the final values of all elements of the lower matrix L including L33.

This is the PDF file used for the illustration of this post.

The previous post: Step-by-step Introduction to Crout’s LU decomposition for a 2×2 matrix.

The next post is A Second option for Crout’s LU decomposition-3×3 matrix.

This is the Omni calculator for estimating various items of linear algebra -LU Decomposition Calculator.

This is a link to another –Calculator for matrices.