Last Updated on February 24, 2026 by Maged kamel
Two solved problems for a 3×3 matrix using Crout’s LU option -1.
We have two solved problems for the 3×3 matrix by Crout’s LU decomposition. For which we will apply the same technique used to derive the elements of the lower and upper matrices. Option 1is finding the lower matrix first.
The following video covers the content of the first solved problem.

The first solved problem for the 3×3 matrix by Crout’s LU-Option-1.
The first problem for the 3×3 matrix is Crout’s LU decomposition. It is required to find both the Lower and upper matrix decomposition LU by using Crout’s method through a given matrix A. The given matrix is 3×3.
We will apply the previous post technique to get the L1 and U1 matrix components by using the following steps.
Step-1 Convert matrix A to a lower matrix (Option 1).
First, we have the matrix A as (1, 1, 1; 4, 3, -1; 3, 5, 3). We will estimate the determinant of this matrix A, which we set to +10. Since the determinant value is not equal to zero, then the matrix is invertible and we can proceed to find L and U matrices based on Crout’s method.
The three elements in the first column vector of the A matrix which are 1 4 3 will be set as L11 &L21 and L31. L11=1, L21=4,L31=3. For U11=a11=1. U12, we will set a12/a11 = 1/1 = 1. While U13=a13/a11=1.
The detailed procedures are shown in the slide image.

Step-2-Derive the values for the L22, L23, and U23-option-1.
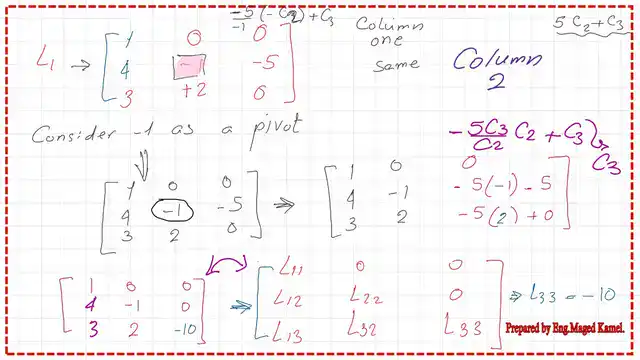
We will use a11 as a pivot, we multiply (-1)*(a12/a11)*column 1 and add the result to the 2nd column, similarly, we multiply (-1)*(a13/a11)*column 1 and add the result to the 3rd column. If we call the new matrix L1, the elements of the matrix are as follows:
The first row is (1, 0, 0). The second row is (4 -1 -5). The third row is (3 2 0). If we compare the first row of L1 to the following matrix, we have (L11 0 0), so L11 = 1. If we compare the second row of L1 to the following matrix, we have (L21 L22 L22*U23), so L21 = 4, L22 = -1, and L22*U23 = -5.
If we compare the third row of L1 to the next matrix, we have (L31 L32 L32*U23 + L33), so L31 = 3 and L32 = 2 and (L32*U23+L33)=0.

Step-3-Derive the value for the L33.
We want to proceed to get the final L matrix; we want to set -5 equal to zero. We use L22 as a pivot. We multiply (-1)*(-5/-1)*column 2 and add the result to the 3rd column. The final elements of the Lower matrix L will be as follows:
The first row is (1, 0, 0). The second row is (4 -1 -5*-1 + (-5)). The third row is ( 3 2 -5*2+(0)). The value of L33=-10. Please refer to the following slide image.
Step 4- Check the product of(L*U)=A-matrix for a 3×3 matrix.
As the final verification step in our series, we multiply L and U to confirm that it reconstructs our original matrix A.”
On the next slide, all the elements in the first column of the matrix are identical to those in the first column of the lower matrix. The diagonals of the U matrix U11=U22=U33=1. L22=-1. U23=+5 while L33=-10. U12=1 and u13=1.
We can write both the lower and upper matrices and check whether multiplying the lower by the upper yields the final A matrix. Using row-by-column multiplication, we can see that L*U equals A.

Elementary matrices to do row operations-first solved problem.
The same steps we have done can be performed by using elementary matrices; the elementary matrix E1 to the right of matrix A will eliminate the a12 and a13 elements. While the elementary matrix E2 will eliminate the a23 element and be placed to the right of the A*E1 matrix, we finally obtain a Lower matrix. Please refer to the following slide image.

We can use the matrices A*E1*E2=L to get the inverse of the upper matrix U. If we multiply both sides by L-1, we can find that E1*E2=U-1.

We can verify that U by U-1 equals I using the data for U that we estimated earlier.

The PDF for the first solved problem can be viewed and downloaded from this link.
The second solved problem-Crout’s LU-Option-1.
Convert matrix A to a lower matrix (Option 1).
The following video covers the content of the first solved problem.

First, we have matrix A as (10 3 4, 2 – 10 3, 3 2 -10). We will estimate the determinant of this matrix A, which is estimated to be +1163. Since the determinant value is not equal to zero, then the matrix is invertible, and we can proceed to find L and U matrices based on Crout’s method.
The second solved problem, the detailed procedure to estimate the determinant, is shown in the next slide image.

Step-1 Convert matrix A to a lower matrix.
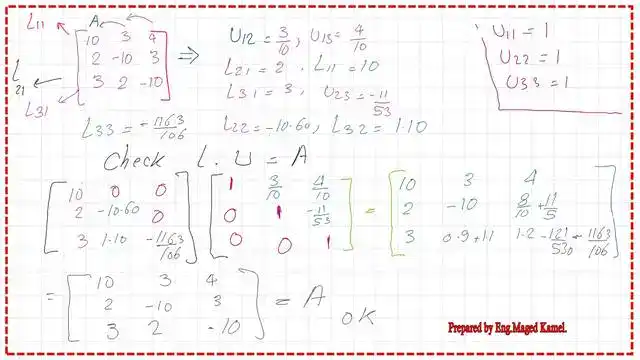
The three elements in the first column vector of the A matrix which are 10 2 3 will be set as L11 &L21 and L31. L11=10, L21=2,L31=3. For U12, we will divide a21/a11 = 3/10. While U13=a13/a11=4/10.

Step 2: Derive the values for the L22, L23, and U23.
We will use a11 as a pivot, we multiply (-1)*(a12/a11)*column 1 and add the result to the 2nd column, similarly, we multiply (-1)*(a13/a11)*column 1 and add the result to the 3rd column. If we call the new matrix L1, the elements of the matrix are as follows:
The first row is (10 3 4). The second row is (2 -10 3). The third row is (3 2 -10). If we compare the first row of L1 to the next matrix, we have (L11 0 0), so L11 = 1. If we compare the second row of L1 to the following matrix, we have (L21 L22 L22*U23=(2 ,-10.6, 8.20).L21=2, L22=-10.6, L22*U23=2.20.
If we compare the third row of L1 to the next matrix, we have (L31 L32 L32*U23+L33), then L31=3 and L32 =.1. To get U23 divide ((2.2)/(-10.6)=-11/53.

Step-3-Derive the value for the L33-Crout’s LU decomposition.
We want to proceed to get the final l matrix; we want to let 2.2 equal zero. We multiply (-1)*(2.2/-10.60)*column 2 and add the result to the 3rd column. The final elements of the Lower matrix L will be as follows:
The first row is (10, 0, 0). The second row is (2, -10.6, 0, 0). The third row is (3, 1.1, -1163/106). As we can see, L33 equals -1163/106.

Step-4-Check the product of(L*U)=A-matrix for a 3×3 matrix.
Using row-by-column multiplication, we can see that L*U equals A.
The complete detailed steps are shown in the previous slide images. At the end, we will check the product L*U against the Matrix A.
Elementary matrices to do row operations-second solved problem.
The same steps we have done can be performed by using elementary matrices; the elementary matrix E1 to the right of matrix A will eliminate the a12 and a13 elements. While the elementary matrix E2 will eliminate the a23 element and be placed to the right of the A*E1 matrix, we finally obtain a Lower matrix. Please refer to the following slide image.

Use elementary matrices to find the inverse of matrix U, since E1*E2 = U^-1.

Verify that U*U-1=I.

The PDF for the second solved problem can be viewed and downloaded from this link.
This is a link to the next post, which introduces the permutation matrix.
References
This is the Omni calculator for estimating various linear algebra items – LU Decomposition Calculator.
This is a link to another –Calculator for matrices.