Last Updated on August 30, 2024 by Maged kamel

Illustration of the Arithmetic Gradient.

The discussion will be about the Arithmetic gradient.

Our new subject for discussion will be the arithmetic gradient, but we will review the relationship between P and F, P is the present- value, and F is the future value. 

Review of the different types of investments.

Deposit money to get the retirement amount at the end of your investment (P/F) relation.

If you deposit money in a bank for the investment of amount=P, for which, you will receive a compound interest i% to get a future  F-value for your investment=F.

We will find that we have different signs, P is represented by a downward arrow, or minus sign since it is a cash-out but, when you receive an F value it will be cash-in and the value is drawn by an upward arrow. The P-value in terms of F, i%, n, and F in terms of P, i%, and n are shown in the slide.

  For the P-value,  it is P=F*(P/F, i%, n). For F- value it is=F=P*(1+i)^n. P- value= F* (1+i) ^-n. The relation is based on annual compound interest i%, but, if we have changed the annual interest to become a quarterly compounded interest. The new interest rate i2=(i1/4%) and raised to the power of 4*(number of years), or 4n. That was the relation of F with a given P, I, and n.

Deposit money to buy a car at the end of your investment (P/F) relation.

There is another relation, for instance, if somebody wishes to buy a car, he or she takes a loan from a bank with interest i% and payment F will be at the end of time n, this is from the bank’s point of view.

Cash in will be with a plus sign  + and the money received F is will be cash-out, with a negative sign (-).

There is another type of relationship when someone receives money to buy goods and pays through installment or uniform series of compound interest after one year of receiving the cash-in for the agreed period. The P-value is cash in or with a positive sign.

The cash out with equal amounts will be cash-out with negative signs, its value =A. The value for A in terms of P, i, n, A=iP(1+i)^n/((1+i)^n-1)), where i is the interest rate, and n is the time in years. The values of A are equal, the same as uniformly distributed load with A value as cash in installments in n the bank account, with an interest I and for some time.

Deposit money as a uniform series to get insured money at the end of an investment (A/F) relation.

For instance, if somebody wants to receive insured money after some time, he will pay equal installments of value  A with an interest rate of i% and for n time, start after one year, the diagram shows that type, the A values are shown as upward cash in and at the end of time, for instance, time=8 years. The F- value received at the end of year 8, can be estimated based on a compound interest i%, the F- value= A(F/A, i%, n), also F=A/i((1+i)^n-1).

The arithmetic gradient factors.

We will discuss a new subject, which is the arithmetic gradient factors.
While paying installments, these installments are not of equal value, but the difference between each consecutive payment is constant and equals  G, which is the same difference between the second and third installments also between the third and fourth installments as well as between the fourth and fifth installments.

After one year of the agreement, somebody pays an installment with the value A. The cash-in diagram has a shape of a trapezium shape, for which the smaller value is A and the larger base=A+4G  for the sketch shown where n=5 years. But if we have n of years, the larger base value of the trapezium will be A+(n-1)G. But if we have n of years, the larger base value will be A+(n-1)*G.

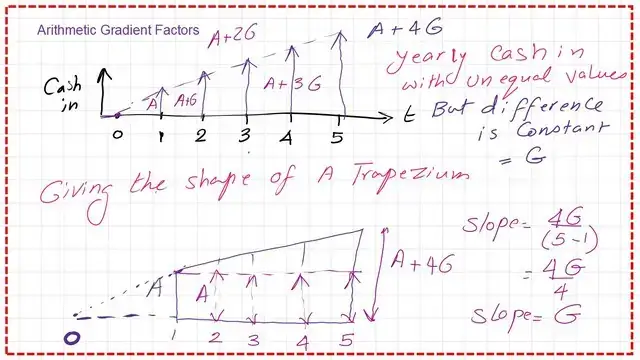
The previous shape consists of a trapezium, which can be solved by converting it into two shapes.

The first shape is an equal installment diagram with a cash-in value of A for 5 years.
The second part is the shape of a triangle with an increasing hypotenuse from 0 to 4G in the case of 5 years, as shown in the sketch, with a slope of 4G/4 =G.
If we want to estimate the future- value in terms of A, i%, n. The relation is F=(A/i)*((1+i)^n-1)). If we want to estimate A in terms of P,  i, n, The relation is F=(i*P)*(1+i)^n/((1+i)^n-1)).

While for the triangular shape, the value for F is in terms of i%, n, G. F=(G/I)*(1+i)^n-1)/I)-n. P/G Find P in terms of G. The( P/G, i,n) has a relation, which is shown in the slide.

External resource in Engineering Economy. This link illustrates different types of economies and how to make economic decisions—the time value of money, Applying Theory to Practice.

The two coming posts are “What is Capital Recovery in the Economy?” and “A Solved Problem for EAW/ Equivalent Annual Worth.”

The third post: Arithmetic Gradient-part 2. How do you find P with the given I%,n, and G?