Solved problem 4-16 for k value for a portal frame.
Full description of the content.
Our solved problem 4-16, from Prof. Alan Williams’s book, Structural Engineering Reference Manual.
It is required to get the effective length factors for two columns, please refer to the next image, two columns are columns NOS 12 and 34.
The sway-inhibited frame means Unbraced frame, Unstiffened frame, and sway frame shown consists of members with identical I/L values.
It is required to determine the effective length factor for two columns which a, he has not included any values for the length of girders or height of columns, we can consider that h and L are the same.
First, we notice that the joint at 1 has hinged support, that was the first remark, the joint at 3, which we consider as far end for girder 23, has no presence of either hinged or fixed joints, this is the normal condition which means we have m=1.
We start to evaluate G values from the Nomograph, starting with joint 2 for column 12. We have only one column, there is no added column at joint 2, then ∑EI/L for columns/∑EI/L for girders, ∑EI/L for girders, *(m).


Our L=h, our condition for column 12, G2=∑EI/L/∑EI/L, then G2=1, joint 2 has only one girder, 23.
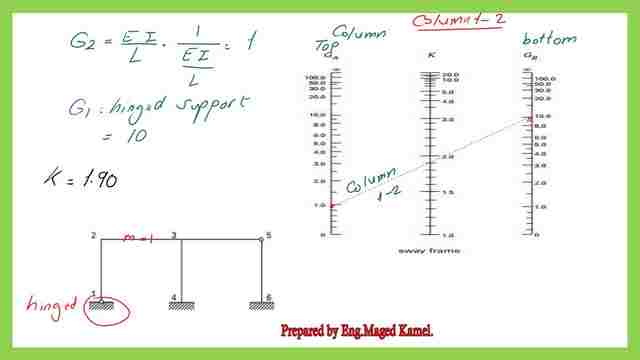
We get G at 2 =EI/L/(EI/L)G at 2 =1, while for joint 1 we have G=10 since it has hinged support. we use the Nomograph.
If we consider12 then 1 will be the G top, we consider as column 21, to get the k value for that column, I considered joint 2 as the top for which G=1, and the bottom joint 1, G=10, draw the line in the Nomograph for the unbraced frame.
Starting from G=1 on the left side and ending with G= 10 on the right side, the intersection with the middle line gives the value of k which is 1.90, please refer to the next image for an illustration.
If we consider joint 1 with G=10 as a top point, and joint 2 as the bottom, k will be the same value. K=1.0. We have completed column 12, for column 34, at joint 3, we have two girders,32-35, the girder 35 ended with hinged support, this is case no.2, where m=1/2.

Let us proceed at joint 3, in the Solved problem 4-16, we have only one column, then G3=∑EI/L for one column- 34 / ∑m*EI/L for two girders, ∑m*EI/L for two girders, which=m1*EI/L for girder 32 +m2*EI/L for girder 35 m for member 32=1, m1=1, no external support attached to that joint, while for girder 35 m2=1/2, since at the far end, there is a hinge the for denominator=3/2*EI/L, G3 =1/1.5=2/3.
For the k value for the column 3-4, in the Solved problem 4-16, one side is G=1, and for the other side G=2/3, joining the two points on the Nomograph for the unbraced frame we get the K for the column 3-4= 1.27, for more details please refer to the next image. For support 4, which is fixed, the code in the commentary lets G=1. We proceed to the nomograph G3 =0.67 as the left point and the lower point as G=1, the intersection will give k=1.27, which was for member 34.


Next time, we will talk about the French equation and how can we use it to get the approximate k value, not the exact value. The solution from Prof. Alan Williams’s book has been included for review, the next subject will be the French equation for the unbraced frame.


This is the pdf file used in the illustration of this post.
A very useful external link is Concentrically Loaded Compression Members.
This is the next post, Solved Problem 4-16 By Using French Equation.

