Solved problem 6-8 for local buckling of columns.
Description of data.
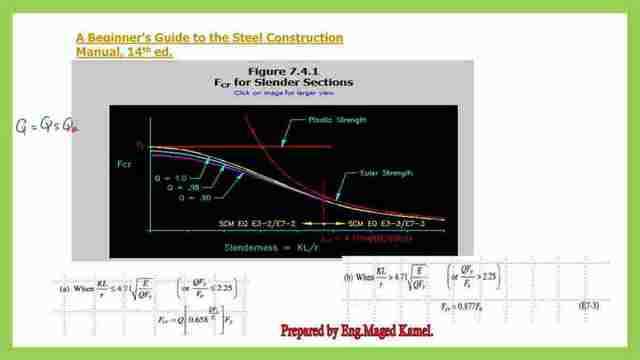
The slide in front of you contains the shapes for various Q values, the Euler graph, and the limiting vertical line for the short and long columns..
Our Fcr value, when Kl/r>4.71*sqrt(E/Q*Fy), Fcr=0.877* Fe.Our Fcr value, when Kl/r>4.71*sqrt(E/Q*Fy), Fcr=0.877* Fes.
. The yellow curve at the left side of the vertical line, for the case of kl/r<=4.71*sqrt(E/Q*Fy), when Qfy/fcr<=2.25, then the fcr=Q(0.658^QFy/Fe)*QFy, and the different value of Qs, from A beginner’s guide to the steel construction manual and the shapes of the graph accordingly.

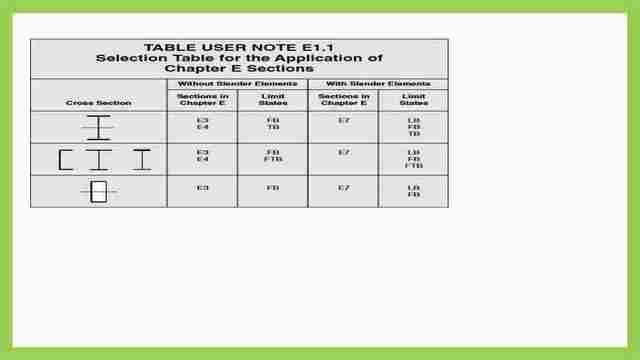
From the next slide, we have Chapter E for the design of members for compression. Part E3 for short and long columns and the table note E1.1, selection table for the application of Chapter E sections.


For the W-section, without slender elements, sections in chapters E, E3, E4′ Limit state, Fb stands for flexural buckling, Tb for torsional buckling.
In the case of slender elements, When λf>λr, where λf flange b/t, λw, web b/t>λrw, then E7 will control the design and relevant parameters. All elements for flexural and torsional buckling. The third item in the next table is the section for the tube section, E3, without the slender section. when λ<λr, as a stiffened section when λ >λr. Then E7 will control, case of slender elements for the limit states local buckling and flexural buckling.

This is the part E7, members with slender elements, the coefficient for the short and long columns, for the item E7-1 till E7-3. The Q=net reduction factor accounts for slender compression elements, Q=Qs*Qa, when our λ>λr for flange and web.
For a cross-section composed of only unstiffened slender elements, since Q=Qs*Qa, since Qa for unstiffened=1, then Q=QS, for the case of an angle, the section is unstiffened.
For cross-sections composed of only, stiffened elements, َQ=Qs*Qa, Qs=1, for the case of a tube, then Q=Qa.
For the general condition for Q=Qa*Qs, For sections composed of multiple unstiffened slender elements.
It is conservative to use smaller Qs from the more slender elements, in determining the member strength from the next slide, for slender stiffened elements, the parameters for Qa and the be, the reduced effective breadth.


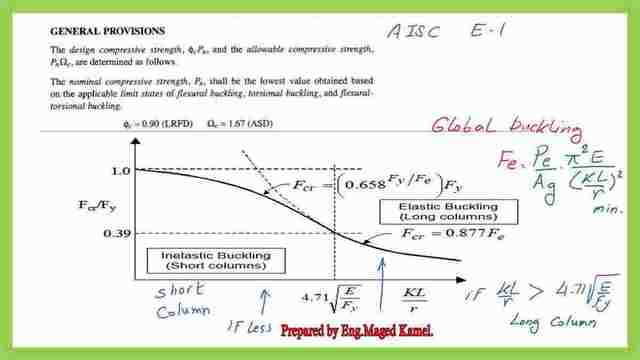
This is the graph for general provisions and relevant equations.

Detailed description for Solved problem 6-8 for local buckling.
For the solved problem 6-8, determine the axial compressive design strength Φc Pn and the allowable design strength Pn/λc of a 24 ft HSS of 14x10x1/4 inch column section, the base of the column is considered to be fixed.
The upper end is assumed to be pinned, Fy=46 ksi, k is 0.7 for the column but the recommended value is 0.8, Refer to table 1-11.
Properties of the HSS section.
We will get a 0.233-inch wall section, the area is 10.80 inch2, b/t =39.9, h/t=57.1, Ix=310 inch4, rx=5.35 inch2,Iy=186 inch4, ry=4.14 inch2.


The same procedure will be carried out, to check whether the column is short or long, so 4.71*sqrt(E/fy )= 4.71*sqrt(29000/46)=118.26, to compare this value to the K*L/r at the y-direction, Kl/r at y=0.8*24*12/ 4.14 =55.652, this is the maximum value as compared to Kl/r x since rx> ry.4.14 inch 2< 5.35 inch2.
The kl/r at y= 55.652 compared to 118.26. Since kL/r at y < 118.26, so the column is a short column, So the Fe will be=92.49 ksi as shown in the figure.


According to Prof McCormac, it is recommended to calculate b=b-3 *tw, so b=10-3*(0.233 =9.301 inch, while h =14-3*(0.233)=13.031, be =0.44736*(25.108)*(1-0.238)=8.56 inch< b, which is 9.301 inch. We had b, after a modification becomes less, which is called be as in the hatched shape, which is= 8.56 inch, then a b-be=9.301-8.56=0.741 inch.


Again regarding the h side since the section is rectangular, the same equation to be used hc=1.92*(0.233) sqrt(29000/46 (1-0.38/(h/t), this time our b in the equation is estimated as h, (1-0.38/(13.301/0.233)* sqrt(29000/46).
The hc should be < h, he= 9.36 inch, which is < 13.301 inch.- solved problem 6-8 for local buckling for columns.
Let us draw h and compare with he side by side, the original h was=13.301 inch.
If we subtract the new he, which is 9.36 inches. The tube contained two parts h and two parts b, the reduction in the h=13.301-9.36=3.94 inch. As two pieces accompanied by a similar two parts calculated. The reduction in the b as (9.301-8.56)=0.75 inch now the =0.75 inch.


The unused part has an area =2(0.75+3.94)*(0.233)=2.1855 inch2=2(0.75+3.94)*(0.233). The area Ae, Ae=10.8-2.1855=8.61 inch2 as a first trial, Q=Qa*1=Qa=Aef/A gross= 8.61/10.80 =0.7976.
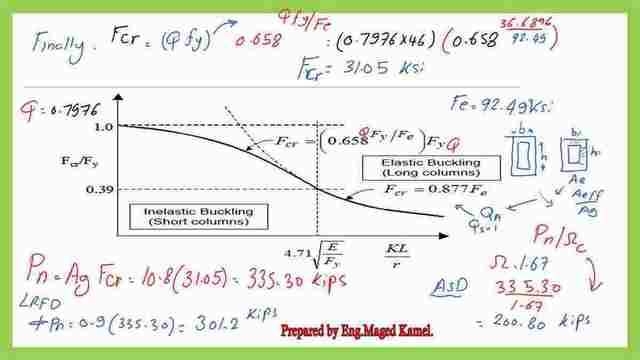
Since the column is short,for fcr calculation, fcr =(Q*fy)*0.658^(Qfy/fe)
since Q=0.7976, fcr (0.7976*46)*(0.658)^(0.7976*46/92.49), Our fe=92.49 ksi, Fcr=31.05 ksi.
Then Pn=Agfcr=10.831.05=335.30 kips.
For LRFd, Φc=0.90,ΦcPn=0.9335.3=301.2 kips.
For the ASD, Pn/Ωc=335.30/1.67=200.80 kips.

This solved problem has discussed the idea that if you have a hollow section due to local buckling as a stiffened element, the section is reduced. Becoming smaller with only be, he as functioning the effective area can be estimated and call it Aef.
The Qa can be estimated as Aef/Ag, then use this Q value, then to the graph to get Fcr.
This is a link to download the pdf file used in the illustration of Solved problem 6-8 for local buckling.
If you link to refer to the previous post: A Solved problem 5-3 for local buckling of columns.
The next post: A solved problem 6-19-4.
For a good external reference, find this link–Chapter 7 – Concentrically Loaded Compression Members.
.

