Last Updated on March 4, 2026 by Maged kamel
Alignment chart-part 2 for the unbraced frames.
Full description of the subject.
We continue discussing the alignment chart, part 2, with the conditions for anti-symmetrical curvature of the unbraced frame.
The Nomograph was based on the assumption of double curvature. At one end, we have a bending moment, but at the other end, another moment, equal in magnitude, will cause anti-symmetrical curvature.
By God’s will, we will discuss the approximate method of the portal frame as the third point.
How can the bending moment for the portal frame be estimated by assuming places of hinges at the mid-span of girders and the condition of the portal frame when having fixed supports?
The fourth point is the m value for the end conditions of the girders in the unbraced frame. If the condition of non-antisymmetric curvature is not achieved, or if the assumptions on which the graph was developed were not followed.
There is an m factor that is determined based on the condition of the girder; what will be its effect on the far end, whether fixed or hinged, on girder stiffness, by multiplying by the m value?
The fifth point is the solved example, 4-5, from Prof Alan Williams’s book.
The sixth point is the French equation for the K value from the nomograph, by God’s will.
Usually, we get Ga and Gb and use the nomograph to determine the k value, which can sometimes be unclear. Using the French equation, we can obtain an approximate value of K that is close to the value reported in the monograph.
Assumptions used in the Nomograph.
The second slide shows the conditions of assumptions from which the nomograph was developed, quoted from the “Structural Steel Design” book.
The behavior is purely elastic in the first item, and in the second term, all members have a constant cross-section. In the third item, all joints are rigid. The AISC includes the same assumptions and explains them in its commentary.
The fourth item, for columns in side-sway, inhibited frames, braced frames, and rotations at opposite ends of the restraint beams or girders, is equal in magnitude and opposite in direction, producing single-curvature bending. On the next slide, we can see a sample of a single-curvature column shape.
For case number 5, Alignment chart-part 2, for the side-sway uninhibited frames (unbraced), rotations at opposite ends of the restraining beams or girders are equal in magnitude and direction, producing double- or reverse-curvature bending.
It is as if the bending moments at the near and far ends rotate in the same direction but have equal magnitudes, and the rotations are opposite, as we will see later. No.6 stiffness parameter L*sqrt(P/EI) of all columns is equal.
No.7 joint restraint is distributed to the column above and below the joint in proportion to the EI/L for the two columns, since we use the summation.
At the common joint, G is estimated as the sum of EI/l for the columns above and below, divided by the sum of EI/L of girders meeting at the same joint.
All columns buckle simultaneously, and no significant axial compression force exists in the beam or girder. There is a p-delta effect, where the beam acts as if it had a compressive force and moment, which reminds us of the eccentricities, whether large or small, that we studied earlier.
I have added a sketch showing the difference between single- and double-curvature columns. It is clear that when a column has a sway, a double curvature is formed, as shown in the last sketch at the right.
For the Nomograph for the unbraced frame, Alignment chart, part 2.
A- Points A and B represent two ends of the A column.
B—For a fixed column, the G value that theoretically approaches zero will be considered equal to 1.
C. For a hinged column, the G value theoretically approaching infinity will be considered equal to 10.
We start with one joint and determine the summation of (EI/L) for columns divided by the summation of (EI/L) for girders meeting at that joint; this is the value of G, which we mark on the graph at the left.
On the other hand, for the different joints for this same column, we determine the summations of (EI/L) for columns divided by the summation of (EI/L) for girders meeting at that joint; this is the value of G, which we mark on the graph at the right. We intersect the middle graph with the value of k required.
The following slide displays the details of the equation for G, along with the various terms used from the AISC commentary.
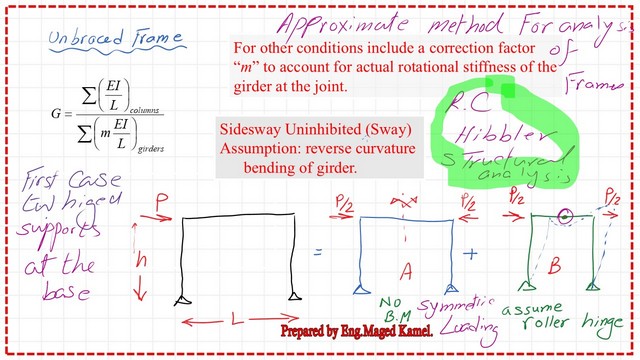
For other conditions, include a correction factor m to account for the joint’s rotational stiffness. For the side-sway-uninhibited, unbraced frame, the assumption is based on the girder’s reverse curvature bending.
Points of contra-flexure.
Prof. Reddy has pointed out that laterally loaded portal frames can be analyzed using the approximations employed, as shown in the figures. For stiff girders, the point of contraflexure or zero moment can be assumed at the mid-height, whereas for flexible girders, it can be considered to be located near the top.
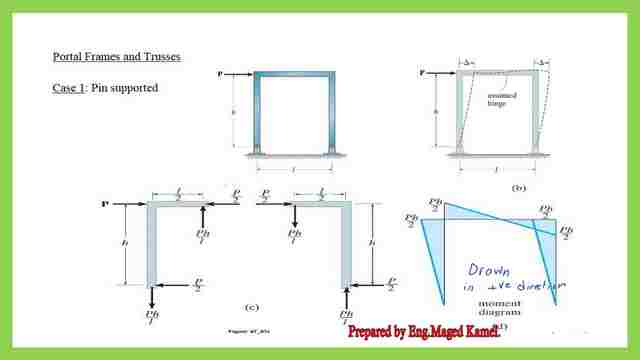
For the portal frame, Alignment chart-part 2, if we act upon by a horizontal load P, while the height of the frame =h, for the case of two fixed support, the behavior as if for elastic curvature as we can see, at the middle, at the middle of the girder we consider as if we have a hinge at the mid of girder and also as if we have a hinge at the mid-height of the column. This will produce a moment diagram in which the shape moment will be reversed at the corner.
In the second case for a flexible girder, the inflection point is near the upper portion of the column, and this is a contra-flexure point for the girder at the middle; the shape of the bending moment will differ, as you can see.
Analysis of a portal frame with a sidesway.
First, we will start with the subject of the portal frame, by God’s will. It is acted upon by a horizontal force P at a distance h from the base, and the span of the girder is L.
From Prof. R. C. Hibbler’s structural analysis. The frame can be considered composed of two parts. In the first part, half of the load will act as anti-symmetric loading at each joint (P/2), and the remaining P/2 will be considered in the second frame.
The total P = P/2 + P/2 for the first frame. In this frame, the P/2 will be opposed by other P/2 acting in the opposite direction of the first frame; there is no bending moment due to antisymmetrical loading. However, for the second frame, P/2 acts on the left joint and the right joint.
We will continue in the next post to solve the same portable frame.
The PDF for this post can be viewed and downloaded from the next document.
This is the next post: A Review of the Portal Frame.
For a good A Beginner’s Guide to the Steel Construction Manual, 14th ed. Chapter 7 – Concentrically Loaded Compression Members.
For a good A Beginner’s Guide to the Steel Construction Manual, 15th ed. Chapter 7 – Concentrically Loaded Compression Members.
For a good A Beginner’s Guide to the Steel Construction Manual, 16th ed. Chapter 7 – Concentrically Loaded Compression Members.