Solved problem 6-19-4 for local buckling of columns.
Solved problem 6-19-4-estimate area and inertia values of the given section.
Determine the nominal axial strength for the Non-standard shape of figure 6.19.4 for an effective length kl=8 feet, fy used is 100 ksi.
The I section is composed of three plates, the upper plate breadth is 10 inches. The thickness is 1/2 inches.
The same dimension is also for the lower plate. The middle plate of height =11 inches, width 1/4 inch, and width= 1/4 inches, thus the overall height is 12 inches.
. Given k*L= 8 feet. Since this section is a built-up section, we can not get information through any tables.
For local buckling, we have to estimate Ix and Iy. The value of rx is much higher than ry, buckling will be governed by the minor direction. We will estimate the Iy, since buckling, will be about the minor axis.
The Iy will be for two plates as 0.5*(19)^3/12*(2)=83.33 inch4, ignoring the inertia of the intermediate section about the y-direction because it has a very small amount, Iy=11(0.25)^3/12=0.014 inch4.
The area can be estimated as two plates area of (105) plus(110.25), Area = 12.75 inch2, then the radius of gyration about the y-direction will be = Sqrt(83.33/12.75)=2.557 inch2.


Check local buckling for stiffened and unstiffened parts.
Check the local buckling, we have two parts, The unstiffened part with 5 inches and thickness is 0.5 inches, the stiffened part with h=11 inch, h/t=11/4.
The equation for λr, is equation b, E7-7, there is a Kc coefficient, For the unstiffened element, if but if b/t <=0.64*sqrt(E*kc/Fy), then Qs =1, if but if b/t >0.64*sqrt(E*kc/Fy) but <=1.17*sqrt(E*kc/Fy), then Qs can be estimated via a new equation, E7-8, but kc is=4/(sqrt(h/tw)), where h is =11 inch, in our example.
h/tw=11/0.25, kc=4/(sqrt(111/0.25)=0.603, Back to E7-7, substitute by the value of kc of 0.603, Fy=100 ksi as given. b/t=10, and the b/t from the equation E7-7= b/t<=0.64sqrt(290000.603)/100) =8.46.


The next step is to evaluate the value of b/t =1.17*sqrt(Ekc/fy).b/t=1.17*sqrt(29000*0.603/100)=15.47.
The un-stiffened section b/t ratio is between 8.46 and 15.47.
The Qs value will be, =1.415-0.615(b/t)sqrt(fy/Ekc), the value of Qs=1.415- 0.615(10)sqrt(100/290000.603)), Qs=0.923, this is the first step for the unstiffened part.


Now, we will proceed to the calculation of Qa. For the slender stiffened element, h/tw=11/0.25=44 will be compared with
(1.49*sqrt(E/Fy), which gives the value of 1.49*sqrt(29000/100)=25.40.
Our h/tw for the section > 25.4, since h/tw>λr, the Qa is <1, since h/tw is >λr. Then the modified h will be based on E7-17.


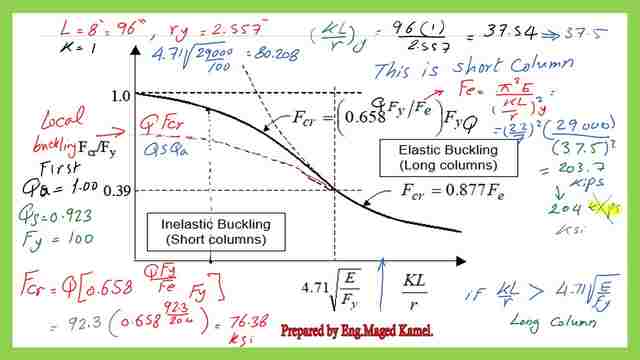
Our f value is taken as fcr estimated but based on Q=1, this f value from fcr=Q*(0.658^Qfy/fe), consider Q=1, where fe=Kl/ry., k*L=8 ft, as given K*L=8*12=96 inch, Kl/ry=96/2.557=37.5, fe=pi^2*E/(kl/ry)^2=204 ksi.
First, consider Qa=1, our calculated Qs=0.923, then q=1*0.923=0.923,for the first trial, Qfy=0.923*100=92.3 ksi, Fcr=92.3*0.658^(92.3/100)=0.923*100=92.3 ksi, Fcr=Qfy*(0.658^Qfy/fe)=92.3* 0.658^(92.3/204)=76.38 ksi.
We have checked earlier, that Our column is short since 4.71*sqrt(E/fy)=80.208. Our kl/ry=37.54, which is < 80.208, so our equation for the short column was modified to include Q in it.
The new graph for the short column is shown as a dotted line.
Take the fcr value which is =76.38 ksi, back to the equation E 7-17 as follows.

Then be=1.92*(tw)*sqrt (E/f)*(1-(0.34/bt*Sqrt(E/f), tw=0.25 *sqrt(29000/f), the trial f=Qa*Fcr as estimated earlier, the trial f=0.923*76.28, Trial f=0.923*76.38=70.50 ksi, the term 1-(0.34/bt*Sqrt(E/f)=1-(0.34/11/0.25*sqrt(29000/70.5)=8.209<11 which is the web height.
After the evaluation, the be is the effective height of web =8.209<11, the original web height, then we will estimate the effective area after deducting the unused areas as follows:
An eff=be*tw=12.75-sum of (b-be)*t, as shown in the equation, b=11 inch, and t=0.25 inch, be=8.209 inch (11/0.25)=44-(8.209/0.25)*0.25^2 =12.05 inch2. This calculation can easily be estimated by taking the flange plate areas plus the be web*t web. Finally, the A eff=12.05 inch2, reestimate the Qa=Aeff /Agr, for the new value of Qa.


Qa=12.05/12.75=0.9452. so the Qnew=Qs*Qa =Qs*Qa , the value of Qa=0.9452 while Qa=0.9452, as per our last calculation & our Qs ia 0.923.
Finally Q new=0.923, multiplied by 0.9452=0.8724, back to fcr =Qfy*(0.685^QFy/Fe), with the new value of Q as 0.8724*100 *(0.658^(87.24/204)=72.94 ksi as a new value of Fcr.
Multiply by Q to get the f new=0.8724*72.9=63.6 ksi. Evaluate the new value of (be ) for the stiffened web.
Qa new =A eff/Ag=12.14/12.75=0.9521, To get the Q=Qs*Qa=0.923*0.9521= 0.879, fcr recalculated with the new Q value
Fcr=72.94 ksi.
be=1.92*(0.25)*sqrt(29000/63.6)* by the other bracket, finally, hw eff=8.557 inch, Recalculate the A eff=10*0.5*2+8.557*0.25, Aeff =12.14 inch2.
Finally As a review, first Q taken =1, Q=Qs*Qa, then log to the short column equation, Get Fcr then multiply its value by Qs.
Estimate The second trial for the h eff, then recalculate the A eff.
Estimate ( h eff) of the web part. A eff is obtained, then divide by the A gross, get a new value of Qa, then get the new Q=Qs*Qa, back to graph get fcr, then multiplied by Q.
A Series of trials was performed until the value of fcr=73 ksi is considered the required Pn is needed.


Solved problem 6-19-4-estimate the nominal load.
In this example for LRFD only, accordingly φc, φcPn =0.9931=838 kips, this is the end of our solved problem 6-19-4.


This is the PDF used for the illustration of this post.
For a useful external resource, please review A Beginner’s Guide to Structural Engineering.
For the next post, A Solved Problem 5-10 For the Available Strength.

