Maximum deflection distance for a simply supported beam Under triangular load-Numerically.
We want to get the maximum defection distance for a triangular load acting in a simply supported beam of length = 6.0 m. The maximum intensity of the load is 20 kNn/m. Our task is to find the x-max distance using the Numerical method. We will solve this by using the Newton-Raphson method for roof findings.
The three equations for the change of slope & slope and deflection values.
This is a list of three items; the first item is the change of curvature equation and the diagram shape for a supported beam under triangular load, where P is the maximum value of the triangular load, x is the distance for which we want to calculate the change of curvature.
The second item is the slope of curvature equation and the diagram shape for a supported beam under a triangular load, where P is the maximum value of the triangular load, and x is the distance for which we want to calculate the slope of curvature. The third item is the slope of curvature equation and the diagram shape, for a simply supported beam under triangular load, where P is the maximum value of the triangular load, and x is the distance for which we want to calculate the deflection value.


The next slide image shows a simply supported beam’s slope and deflection equations under a uniformly Triangular distributed load.
It is required to estimate the maximum deflection distance from the left support x max. The point of the maximum deflection is the point for which the slope of curvature is zero. Normally, we use the Newton-Raphson method we want to get the point where Y value =0.
The function value f(x) was on the numerator side, rerefer to the relation, where X0 is the starting point, f(x0) is the function value at x0, f'(x0) is the slope value of the function at point X0.
The revised form of the Newton-Raphson equation is based on the slope equation.
To use the Newton-Raphson equation, we are going to deal with the y’ curve, since it is changing from a +ve value to a negative value, then a root point for zero slopes will give us the point of maximum deflection, instead of dealing with y curve as in the case of the original form of Newton-Raphson equation, we are now dealing with y’ function.
The steps for estimating x max by the analytical solution.
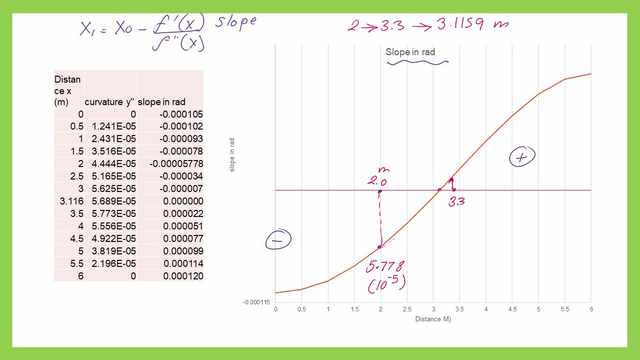
The modified equation for the root point will be as, for the first point after setting an initial point of, which will be given a value of 2.00m, less than the L/2.
Our first trial value of x0 is =2.00m.
We need f'(2) and f”(2) to apply it in the adjusted equation. We have the expression for F'(x) for the slope value of the curve due to the triangular load also y” the change of curvature of the beam. We plug in with x0=2.0m and get the two values of f'(2) and f”(2), as shown in the next slide. We need to use 1/EI=1/8*10^4.
Our first x0 with a starting value of 2.0m will lead us to a modified value of 3.30m, as the maximum deflection distance. along with y’ function.


Our second trial value of x0.
Then we plug in with x0 as a second trial=3.30m, we get the second value for the maximum deflection distance of 3.1169 m. Our third x0 with a starting value of 3.1169 m will lead us to a modified value of 3.1159778m, as the maximum deflection distance.


Then we plug in with x0 as a second trial=3.1159m, we get the third value for the maximum deflection distance of 3.115977 m.
The following table shows the result of x0 when we start with an initial point of 2.0m for four iterations.


This is a graph of the slope, we start with a point with x=2m it will lead us to another point with x=3.30 m, please refer to the previous table.

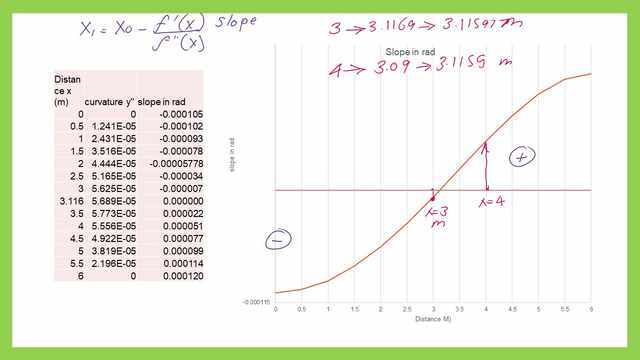
In case our first trial value of x0 is =3.00m.
If somebody wishes to choose a starting point as=3.00m. x0 with a starting value of 3.0m will lead us to a modified value of 3.1166m, as the maximum deflection distance.
Then we plug in with x0 as a second trial=3.1166m, we get the second value for the maximum deflection distance of 3.115977 m.
The following table shows the result of x0 when we start with an initial point of 3.0m for four iterations.
If somebody wishes to choose a starting point as=4.0. x0 with a starting value of 4.00m will lead us to a modified value of 3.09m, as the maximum deflection distance.
Then we plug in with x0 as a second trial=3.09m, we get the second value for the maximum deflection distance of 3.1160 m.
The next slide contains a table for the values of slope according to x values. In the iterations, we used x=3m and x=4m and both led to x=3.1159m based on Netton-raphon method.

This is the previous post-structural analysis numerically by the Newton-Raphson method.
This is a good external reference. Holistic numerical method.
This is a useful link for a numerical analysis calculator.

