Last Updated on September 1, 2024 by Maged kamel

Solved Problems For P-F Value Relation.

Solved problems for P-F, and F-P.

There are Three solved problems for P-F Value.

A problem 3.5 to estimate the future value for a given present value, time, and interest.

We have a solved problem 3.5 from Newnan’s book, Engineering Economic Analysis, if $500 were deposited in a bank savings account, how much would be in the account for three years hence if the bank paid 6% interest compounded annually?

We draw a diagram, the x-axis is for the time, we divide time into, three spaces starting from 0, or time now, spaces starting from 0, or time now,  the cash deposited is $500, and we draw a downward arrow.

For the Future value at the end of 3 years, it is represented by an upward arrow.
The relation between the future value and the present value states that F=P*(1+i)^n.

The P-value is the present value=$500,  i=6% n=3 years, we will substitute F=500*(1+0.06)^3=$595.51. The future value F, which we have estimated, is shown as a downward arrow since the bank will pay this value.

The diagram has 3 spaces as 0,1,2,3 in years, i=6%.
By symbols, the same value is obtained as F=P(F/P,i=0.06,n=3)=5001.06^3=$595.508.

The second solved problem 3.6 of the solved problems for Present/Future Value.

How to determine the p-value from a given F-value, n, I%?

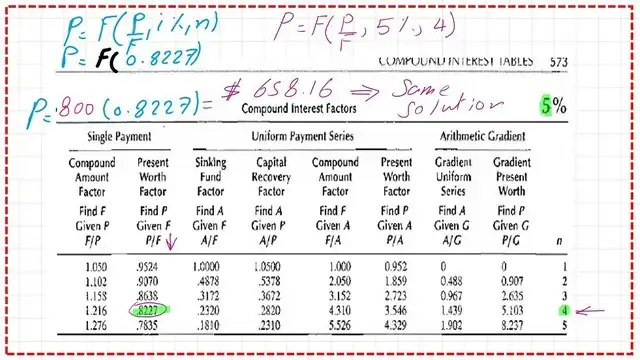
This is the second solved problem of the three solved problems for P-f, quoted from Prof.Donald G Newnan’s book, Engineering Economic Analysis. If you wish to have $800 in a savings account at the end of 4 years, we draw in time scale, 4 equal spaces as 0,1,2,3,4, the F value is shown as an upward arrow=$800 at the end of year 3, and the 5% interest, was paid annually, i=5%, n=4.

How much should you put in the savings account now? P at time 0 is unknown, shown as a downward arrow.

If F=P(1+i)^n, readjust the formula to be  P=F(1+i)^(-n), For F=800, i=0.05, n=4. We substitute, to get P=800*(1+0.05)^-4, or P=800/1.05^4=$658.16, this is the money to be deposited in the bank to get $800, notice that P-value is<F value.

There are tables from which we can estimate the compound interest factors.
For the case of interest rate I=5%, to get the present worth factor P/F under a single payment, find P with given F, we use a table, with  I=5%, n=4, which is highlighted by a yellow color.

We draw a line from n=4, proceed to the left, then the value of P/F can be found, as 0.8227.
That is the direct method by using tables to get the P-value with a given F.

A solved problem 2.2 is how to find the expected investment at time 0, for a given investment future value, the cost of money is given.

The third solved problem 2.2 of the three solved problems for Present/Future Value.

How to determine F-value from a given P-value, n, I%?

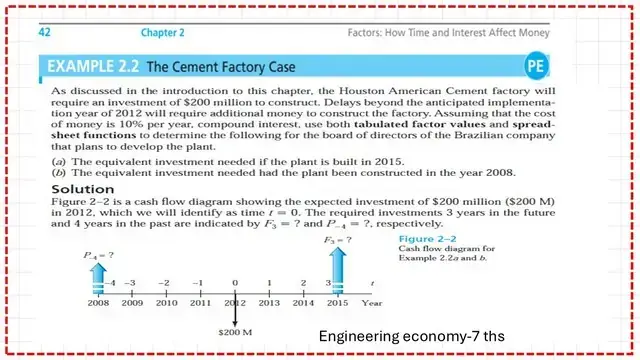
This is the third solved problem of the three solved problems for P-f. Solved problem 2.2- As discussed in the introduction to this chapter, the Houston American Cement factory will require an investment of $200 million to construct. Delays beyond the anticipated implementation year of 2012 will require additional money to construct the factory.

Assuming that the cost of money is 10% per year, compound interest, use both tabulated factor values and spreadsheet functions to determine the following for the board of directors of the Brazilian company that plans to develop the plant.

(a) The equivalent investment is needed if the plant is built in 2015.
(b) The equivalent investment needed had the plant been constructed in the year 2008.

We have a time interval from 2012 to 2015, these are three years.
The table of i=10% is used, n=3.

We will estimate the F from the relation, F=P(F/P, i,n) F=200(F/P,10%, n=3) from the table, F/P=1.3310, then multiply by $200 millions& F=200*1.3310=$266.20.

Using an Excel sheet to solve for the P-value and F-value.

A solved problem 2.2 how to find the expected investment at time 0, for a given investment future value, the cost of money is given, but using an Excel sheet? If we want to use the Excel sheet, make a new table P=$200 in millions, i=10%, n=3, this is for part a) of the solved problem. The result obtained is the same.

The function used is FV (10%,3,,200) with two commas.
For the second part of the solved problem, we have F=$200 million, i=10%, n=4, and the present value is unknown.

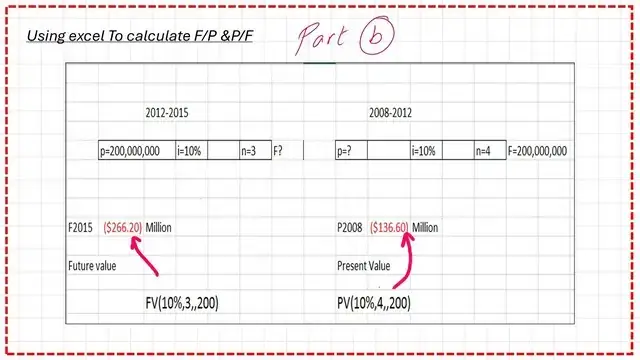
The related excel function is  PV(10%,4,,200)=$136.60.

We will use the table for n=4, which is the difference between 2012& 2008, I=10%,P=F(P/F,i,n)=P/F=0.6830, P=200*0.6830=$136.60 million.

For a useful external resource, Engineering Economy. Applying Theory to Practice.

The next post 6- Easy approach to compounding technique.