8-Introduction to Crout’s LU decomposition for a 2×2 matrix.

Last Updated on January 13, 2026 by Maged kamel

Introduction to Crout’s LU decomposition for a 2×2 matrix.

The elements of the 2×2 upper and lower matrices can be obtained using the Gauss elimination method. Next, we show how to solve for x and y in two equations using the lower-upper triangular method through an example.

Video for the content of the post

There is a brief description of the post’s content.

Step-1- Derive the expression for Crout’s LU decomposition for a 2×2 matrix.

If we have a 2×2 square matrix, we call it matrix A. If it is invertible, it can be expressed as the product of two matrices. One of these is called the lower Matrix. The other Matrix is the Upper Matrix.

The lower Matrix is expressed as lij. Where I represent the row, and J represents the column. We have a total of 6 unknowns. For the lower matrix, we have three unknowns: these are L11, L21, and L22. For the upper matrix, there are 3 unknown elements: U11, U12, and U22.

In The Crout’s method, U11 = U22 = 1. In a 2×2 matrix, the lower Matrix has L11, L22, and L21 nonzero. Unlike the previous method, Doolittle’s LU decomposition, Crout’s LU decomposition for the 2×2 matrix assumes that the upper triangular matrix elements U11 and U22 are equal to 1, whereas the L matrix’s diagonal elements are not 1. Our unknowns become only four. Please refer to the following slide image.

Step 2: The values for the L and U matrices for Crout’s LU decomposition for a 2×2 matrix.

Since A  is represented by the multiplication of the lower multiplication by the upper matrices, we will perform the multiplication of the lower and upper matrices and equate the product to the elements of matrix A.

 The product of the First row by the first column can be expressed as L11*u11 = a11.

The product of the First row and the second column can be expressed as (L11*U12)+0=a12.

If we multiply the second row by the first column, we can write (L21)*U11+0 = a21. If we multiply the second row by the second column, we can express it as (L21*U12) +L22* U22 = a22.

From equations I and II, we have L11 = a11 and L21 = a12. From equation III, we get U12 = a12/a11. Finally,L22=a22-(a21*(a12/a11)). Please refer to the following slide image.

Based on the previous equations, derive a technique for the matrices L and U from matrix A. If we keep a11 and a21 as elements of L11 and L21, and set U11 = a11/a11 (which equals 1) and U12 = a12/a11 for the elements of the upper matrix U, then U22 = 1. For L22 will be set equal to a22-U12*L21.

Please refer to the following slide image.

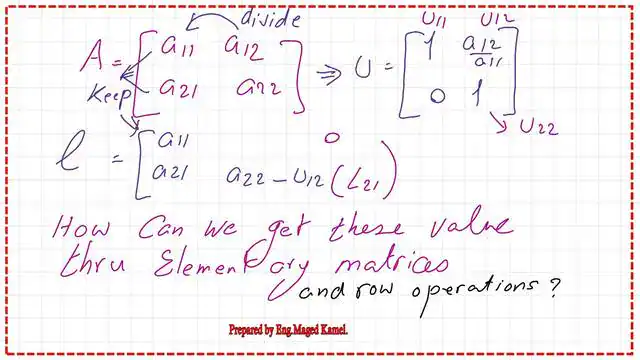
We can use two options to obtain the elements of the lower and upper matrices; we will start with the first option.

Step-3-Option-1 Convert A to a lower matrix.

To Option-1 Convert A to a lower matrix; If we express L by U as a matrix that has elements( L11, L11*U12, L21, L21*U12+L22), converting such a matrix to a lower matrix is achieved by multiplying by a permutation matrix that has ( 1-l11U12/L11, 0, 1), which will create the lower matrix L. Please refer to the following slide image.

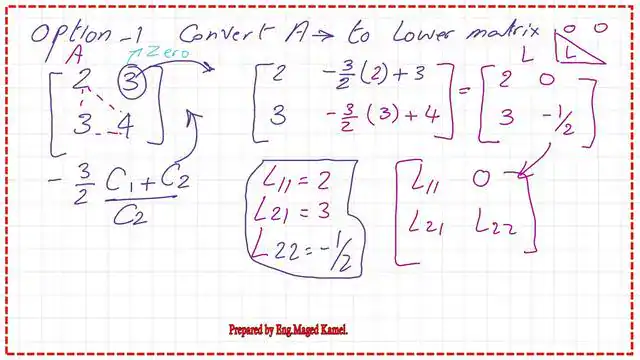
We use numerical values for the matrix A; we write A = (2 3 3 4), meaning a11, a12, a21, and a22.

We apply this information to the given matrix A, which is (2, 3, 3, 4). The first column will be placed as the first column of the L matrix. The L11= a11=2; the L21=a21=3. To set L12 to zero, we use a11 as the pivot. We will multiply the second column by (-3/2)*C1 and add the result to it. The value of L22=-(3/2)*3+4=-1/2.

We need to have the value of L22. For the U matrix, we have U11 = U22 = 1, while U12 = a12/a11 = 3/2. Perform the row echelon to convert matrix A to an upper matrix, taking the value of U22 as the value of L22—the final value of L22=-1/2. Please refer to the following slide image.

Step-4- Multiply matrix A by an elementary matrix E1 for a 2×2 matrix to get the L matrix.

To get the L matrix, we multiply matrix A, from the right, by an elementary matrix E1, with elements of ( 1, -3/2, 0,1). To obtain the upper matrix, we compute the inverse of E1.

The inverse is (1, 3/2, 0, 1). We can estimate the value of matrix C by multiplying L-1*B, where L-1 is the (2×2) matrix we just estimated, and B is the (2×1) matrix with entries (13, 18). As we can see, C = (13/2 3) is a 2×1 matrix.

There is proof that the Upper matrix is the inverse of the E1 matrix, as shown in the following slide.

Step A- Use option 2- Convert matrix A to an Upper matrix for Crout’s LU decomposition for a 2×2 matrix.

To get the U matrix, we multiply matrix A, from the left, by an elementary matrix E, with elements of ( 1, 0, -L21/L11,1). The elements of the U matrix are (L11, L11*U12, 0, L33). Then multiply by -C21*C11/(C11)+C21 to get the value of U12, as we will see in the next example.

Use row operations to get the Upper matrix U.

We will use the matrix A = (2, 3, 3, 4) and perform row operations. Keep R1 unchanged, use a11 as a pivot, multiply R1*-a21/a11, and add the result to the second row to eliminate a21.

L11=2, L11*u12=3, L22=-1/2, U12=3/2. Please refer to the following slide image.

Use elementary matrix E1 to get the U matrix.

We will do the row operations by using the elementary matrix E1 that we multiply matrix A from the left side, E1 elements are (1,0, -3/2,1); the previous values for L11, L22 and L11u12 are obtained.

Get the values for x and y from matrix C for Crout’s LU decomposition for a 2×2 matrix.

We have two equations for which we want to develop Crout’s LU decomposition for a 2×2 matrix. The first equation is (2x+3y=13) and the second equation is (3x+4y=18).

As we can see, the determinant of the matrix equals -1, not zero. We use the same values for the L and U matrices to represent the A matrix.
The final value of X – the matrix can be estimated as a (2×1) matrix, 2 3). We will check whether our given equation satisfies the

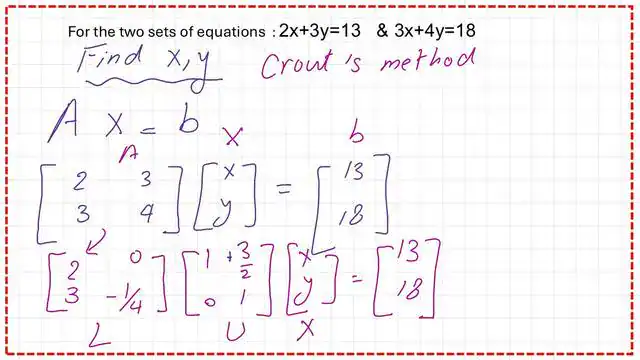
Get the values for the C matrix for Crout’s LU decomposition for a 2×2 matrix.

We use the expression for C-U*X, then L*C=B. Multiply both sides by the inverse of the L matrix, and we get C=L-1*B. The inverse of matrix L is (1/2,0, 3,-1/2). C matrix is found to be equal to (13/2,3). We can find the inverse of the U matrix as (1,-3/2,0,1)

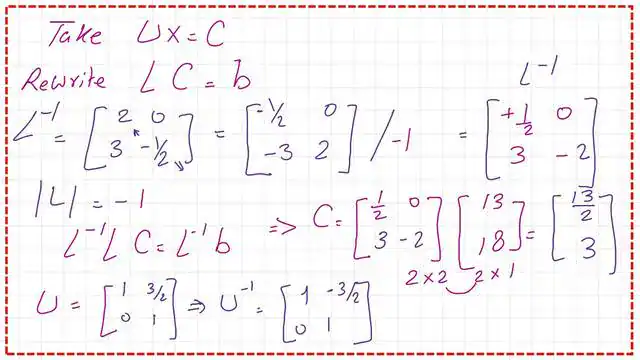
For the expression of U*x=c, if we multiply both sides by U-1, we get X=U-1*C. Finally, we get x = 2, y = 3. We will check these values in the linear equation, and these values are satisfied.

We can use L*U*X=b multiply both sides by U-1*L-1*, we get X=U-1*L-1*b. Please refer to the following slide image.

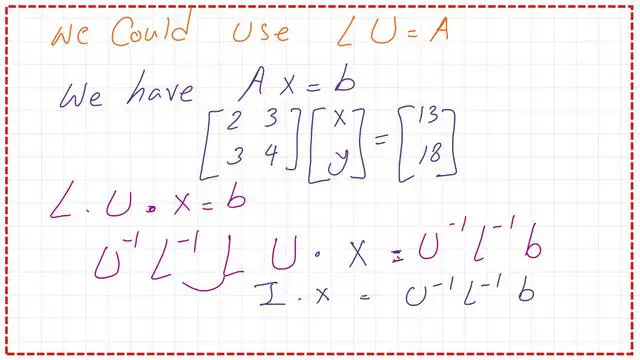
The full data for the Unknowns, using the multiplication U-1*L-1*B, are shown in the next slide.

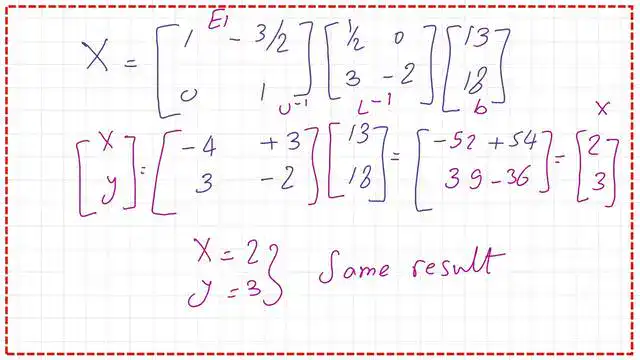
Final check for the validity of the solution for the two simultaneous equations.

The PDF data for this post can be viewed and downloaded from the following document.

The following post is Crout’s LU decomposition for a 3×3 matrix.

This is the Omni calculator for estimating various linear algebra items – LU Decomposition Calculator.

This is a link to another –Calculator for matrices.