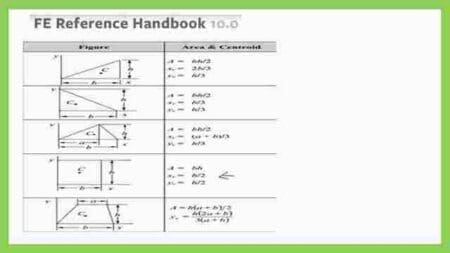
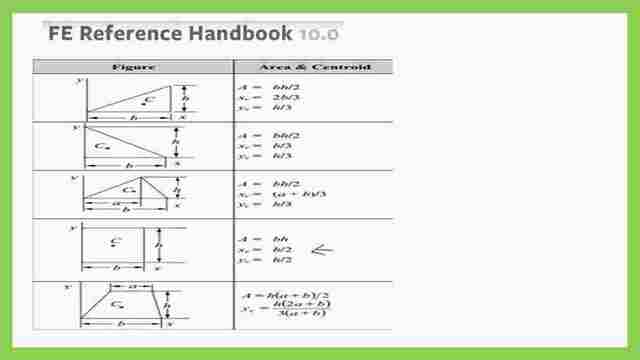
Area and Cg for a rectangle.
Reference handbook 10.00 value for area and Cg at the x- direction.
To get the area and Cg for a rectangle, we will integrate an infinitesimal area of (dx) width and dy height, about the external axes. It is required to get the same data as obtained from the FE reference handbook as attached in the next slide image, where Xc=b/2. Xc, we call it X- bar.
This is a picture from the FE reference handbook for the area and Cg of the different plain shapes.
Area and Cg for a rectangle in the x- direction-(x-bar).
Our new topic will be the estimation of the area and Cg of a rectangle. The procedure will be done by integrating a strip of the area of(dx*dy), the summation of this tiny area will be equal to the total area.
The summation of this area’s first moment at the Y-axis will give the first moment of the area of the whole rectangle at the y- axis.
But the double integration will include two operations, the first operation will be the integration of dy from y=0 to y=h, thus a rectangular strip will be created, then the moment of the strip about y will give the final value of the first moment of area of the rectangle at the Y-axis.
The detailed calculation for the first moment of area for the rectangular shape is presented in the next slide image. The final value of the first moment of the area at the y-axis will be h*b^2/2.
The final value of x- bar will be obtained by division of the value of the first moment of the area by the value of the rectangular area.
The area of the rectangle will be the product of the base by the height, which is =bh. The final value of x- bar=b^2h/2/(0.50bh)=b/2, or half the breadth, the result will match the Reference handbook value given.
Reference handbook 10.00 value for area and Cg in the y- direction.
To get the area and Cg for a rectangle, we will integrate an infinitesimal area of (dx) width and dy height, about the external axes. It is required to get the same data as obtained from the FE reference handbook as attached in the next slide image, where yc=h/2. yc we call it y- bar.
Area and Cg for a rectangle at the y- direction-(y-bar).
Now we will estimate the first moment of area about the x-axis. The procedure will be done by integrating a strip of the area of(dx*dy), the summation of this tiny area will be equal to the total area.
The process is done by using the double integration method, the full details are shown in the next slide images.
Likewise, the summation of this area’s first moment at the x-axis will give the first moment of the area of the whole rectangle at the x-axis which will be =b*h^2/2.
The final value of the y- bar will be obtained by the division of the value of the first moment of the area by the value of the rectangular area.
The area of the rectangle will be the product of the base by the height, which is =b*h. The final value of y- bar=h^2*b/2/(0.50*b*h)=h/2, or half the total height f the rectangle, the result will match the Reference handbook value given. Thus the final value of area and Cg for a rectangle is completed.
Another alternative is considering a vertical strip of breadth dx and height =h and performing an integration about the y-axis, it will be a single integration, and we will get the same result for the x-bar.
Another alternative is considering the horizontal strip of breadth b and thickness =dx and performing an integration about the x-axis, it will be a single integration, and we will get the same result for y-bar.
This is a link for the pdf file used in the illustration of this post.
For a good external reference, please refer to the Centroid of an Area by Integration.
The next post will be Area and Cg for a Trapezium.