37-Solved problem 8-33 for Plastic nominal Uniform Load.

Last Updated on June 7, 2024 by Maged kamel

Solved problem 8-33 for a plastic nominal uniform load.

Solved problem 8-33 estimate the nominal load Wn.

In solved problem 8-33. The given section of the beams is W16x26. It is required to get the value of W_n, the plastic nominal uniform load,  from table 1-1, we get the value of the plastic section modulus Zx, which is 44.20 inch3.

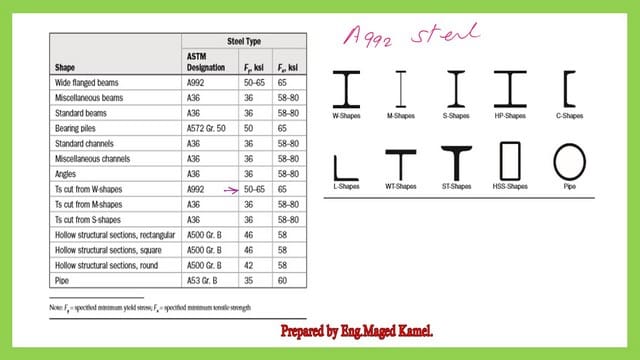
The given yield stress for steel is 50 ksi; please refer to the second slide image.

The nominal, which is the plastic moment value Mn, is equal to Mp=Fy*Zx= =50*44.20/12=154.166 Ft.kips. Because we will use MASTAN 2 to compare with our estimate, the Mn value is written as equal to 2210 kips.

A list of different types of steel and their Yield stresses.

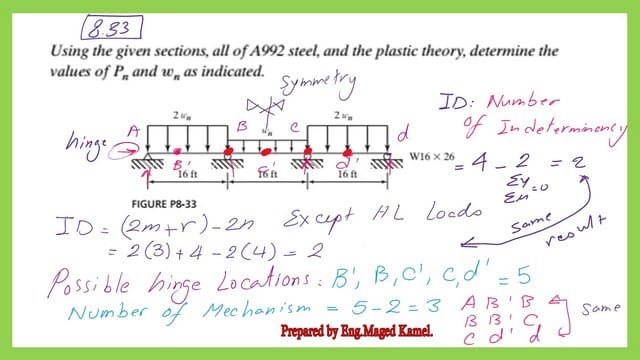
Solved problem 8-33-Number of possible mechanisms.

We need to estimate the number of indeterminacies for the given system of beams. There are two possible ways. The first way is to disregard the horizontal loads and find the number of vertical and moment unknowns.

The number is 4. We will deduct the number of equilibrium equations, which are ∑ Y=0 and ∑ M=0. The difference will be equal to 4-2=2.

The second way is to disregard the horizontal loads and use the equation 2m+r-2n), where m is the number of members, which equals 3. The r is the reactions, 4, while n is the number of nodes, which equals 4.

The ID number will equal 6+4-8=2, the same value as estimated from the first method.

The next question will be, what will be the number of possible plastic hinges? The possible hinges are 5. Deduct 2 from the 5; we get three, which is the number of mechanisms.

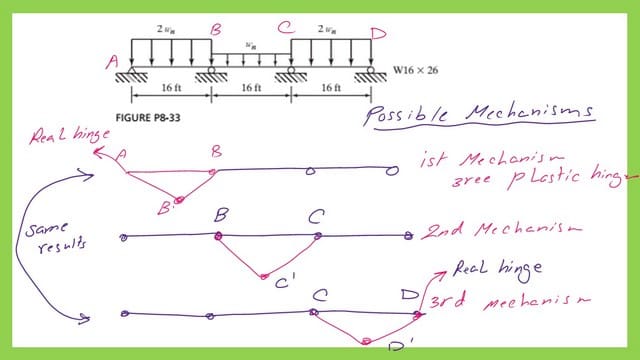
The next slide shows the details of the three mechanisms that we will investigate. The first and last Mechanisms are similar.

What is the X distance value for shear for the first span and the Wn value?

What is the distance x from the left support to the point of maximum Mp? it will be the point of zero shear.

We have beam AB with a plastic moment Mp at the right end. The reaction RA is equal to 2wn*(L/2)-Mp/L. To have a zero shear, we get the relation of wn*L-Mp/L=2*Wn*x. We readjust the equation to give a value of Mp.

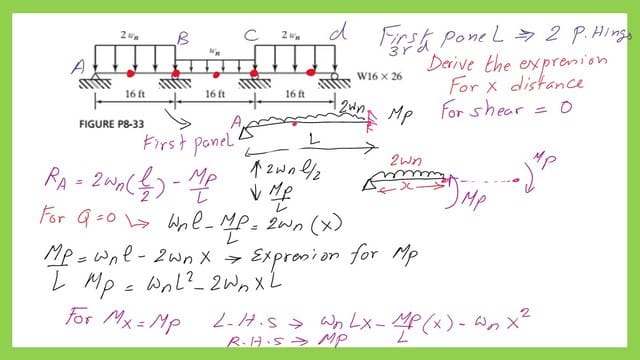
We can derive a relation between Mp and Wn by looking at the plastic hinge. And equate to Mp. We substitute the value of Mp, which has been obtained, and Derive an expression of x. The x value will be equal to 0.414*L

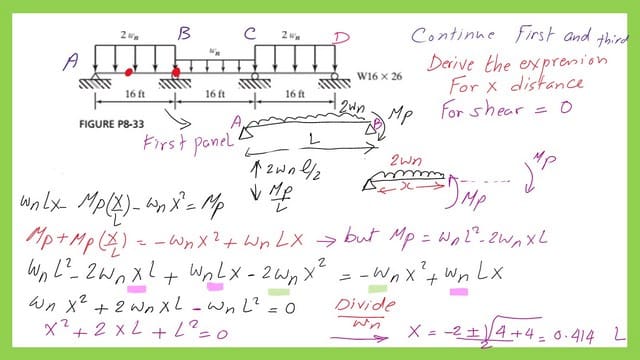
We will substitute for the value of x, and we have Mp equal to 184.167 ft. kips. Finally, we get the Wn value equal to 4.193 Kips /ft.

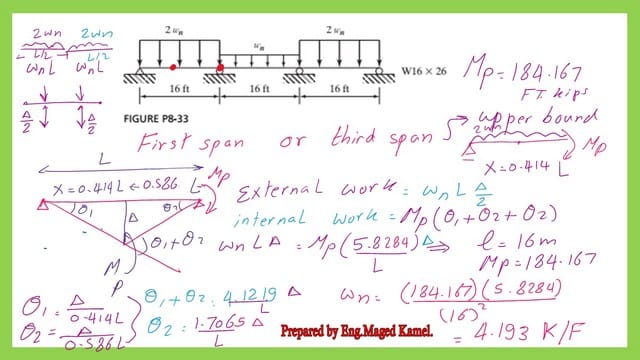
Check the value of Wn using the upper bound method.

If we have a span distance L=16′, then the x distance to the plastic hinge=0.414*(16)=6.624′. Due to the failure mechanism, a deflection will occur by a Δvalue.

For the first span, the distance to the maximum deflection is 6.624′ from the left support.
The remaining distance to the right support is (16-6.624)= 9.376′. We have two angles θ1 and θ2. θ1=Δ/0.414L, for θ2= Δ/0.586 L.

We equate the external work with the internal work. The next slide image shows the full data for the estimate of Wn, which equals 4.193 Kips/Ft.

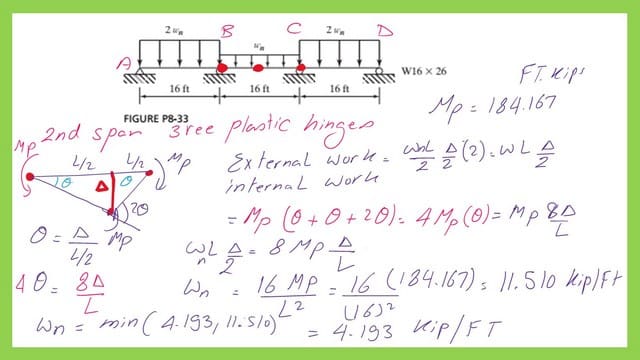
Solved problem 8-33 estimate the plastic nominal load Wn for the 2nd span.

The second span can be considered a continuous beam from both sides.

Due to symmetry, we have 2*Mp at the two edges and one Mp at the mid-span. We will check the internal work. The second span =16′. We have three Mp acting as shown in the sketch. Due to deflection, we will have an angle θ at both sides. For θ =Δ/8.The value of 2*Δ=Δ/4.

The external work is =Load* span * average deflection=Wn*16*Δ*0.50. The internal work= Mp(θ) +Mp(θ)+Mp(2*θ).

The total value of the internal work =4*Mp*θ. The external work=internal work, W_n=Mp*(1/16). The nominal Wn is estimated from the second span=Mp/16=0.0625 *MP. Mp is the M-nominal of the given section W16*26. The Wn value will be equal to 11.51 kips/ft.

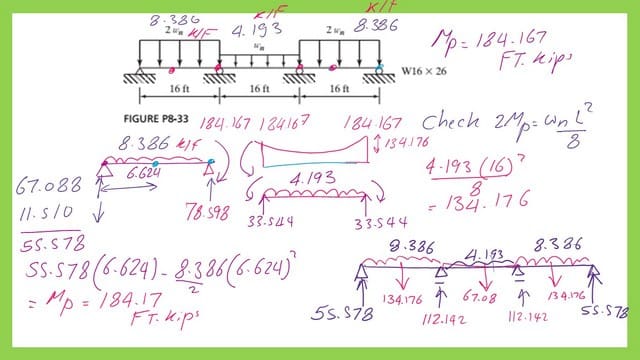
We have two values for Wn, the first one 4.193 kips/ft, while the second value is 11.51 kips/ft we will select the lesser value which is 4.193 kips/ft. That is the value for the nominal uniform load for the three spans. But the first and third spans will carry a nominal uniform load=2*41934=8.3868 Kips/Ft.

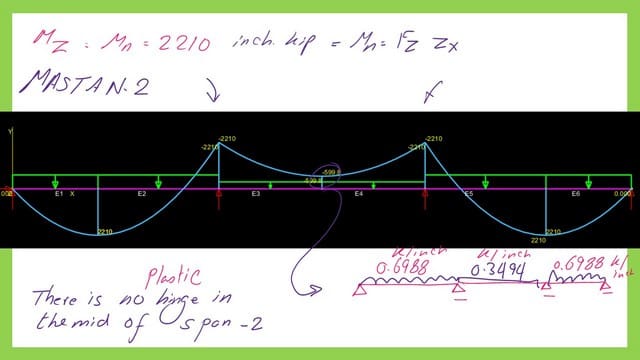
Investigate the middle span, we have no plastic hinge at the middle.

We have a plastic hinge in the middle of the second span Bc because we have a moment value of (+184.176-134.176=49.991 Ft. kips, which is less than Mp.

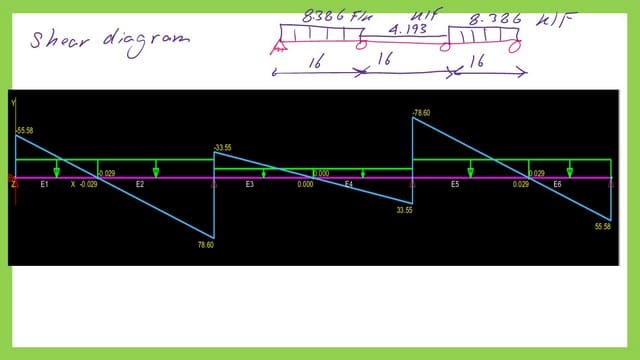
I have included the shear force diagram for the three spans due to the nominal Wn loads.

Use MASTAN 2 to estimate the value of Wn.

We can use MASTAN2 to get the nominal uniform load. The E value is 29000 ksi, and Fy=50 ksi. Since we need to find Wn, we must adjust the beam spans to inches and the uniform loads to kips/inch.

I consider a working load of 0.20 kips/ft, 0.40 kips/inch for the first and third spans, and 0.20 kip/inch for the mid-span.

After making the first order inelastic, the lambda value needed to create a mechanism is 1.747. The nominal load Wn will be equal to 2*1.747=0.3494 kips/inch, which is equal to 4.1928 kips/ft, which is the same as our calculation.

The first and second hinges are created due to a load of 0.3322 kips/inch. Please refer to the next slide for deflection and places of plastic hinges.

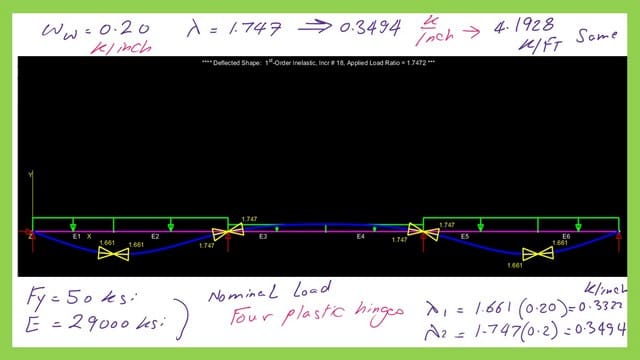
We can check that we have first and second plastic hinges when the Bending moment equals Mp at Wn value equals 7.9728 kips/ ft.

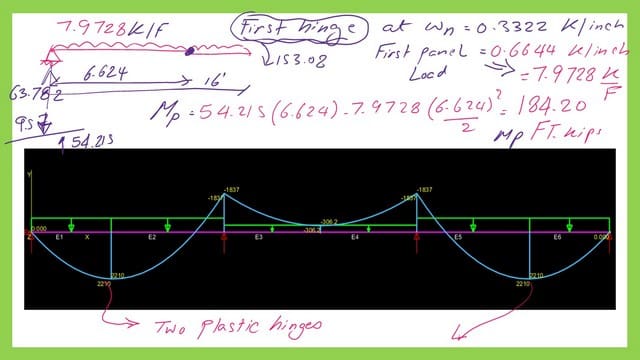
The next slide shows the moment values for the second span.

In the next slide, we can check the shear value of the three beams using MASTAN 2. Thanks a lot, and I hope this post is useful.

Have more information about the structural analysis –III.
This is the next post, 37a-solved problem 8-34– How to get Wn value for three-span beam?