Practice problem 5-2-3-verify Zx for W18x50
Practice Problem-5-2-3-verify Zx for W18x50.
Verify the value of Zx of the W section W18x50, which is tabulated in the dimensions and properties Tables in Part 1 of the manual. We will consider two ways to estimate the Zx of W18x50.
The first method considers the W section as composed of two Wt sections. each Wt section is WT 9×25.
The second method considers the W section as an assembly of three plates and finds The Yct and the At/2 values.
We can represent the W18x50 as two Wt sections assembled.
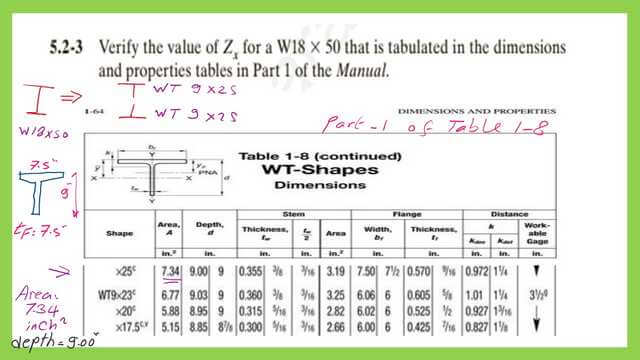
As seen in the sketch, each Wt is 9×25. Table 1-8 of the manual has two parts. Part 1 gives us the dimensions of the Wt section. The breadth and thickness of the flange, as well as the overall height and thickness of the stem, are important.
From part 1, I need to know the area for Wt 9×25, equal to 7.34 inch2, and the depth of the wt section, which is 9 inches.
The distance Y bar from the top of the WT9x25.
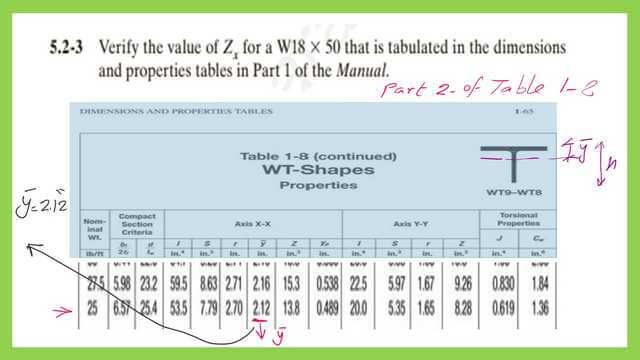
In the next slide, there is part 2 of Table 1-8, from which I need only the value of the y bar, which is the distance from the top of the flange to the Cg of the section. The value is 2.12 inches.
I drew the W section on the third slide, assembled from the Two WT sections. In this section, we can find the value of the YCt or the distance from the compression and tension forces, and each force acts on the CG.
The Yct value equals ( d-2y bar), where d is the overall depth of the W18x50 section, the y bar we got from the previous slide. Then, the distance YCT value is equal to 18-2*2.12=13.76 inches. The area of At/2 equals 7.34 inches2, which we obtained from Table 1-8. We apply the equation of Zx equal At/2*(yct)=7.34*13.76=101.0 inch3.
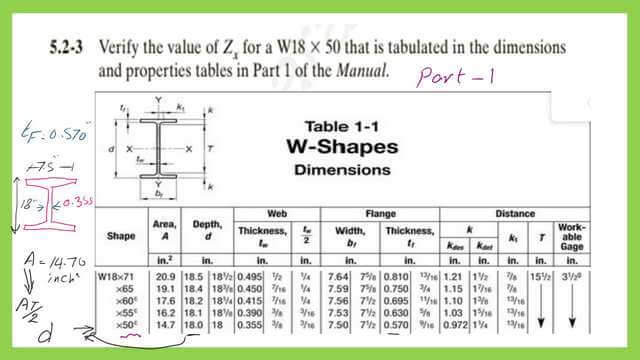
The next slide shows two parts of Table 1- 1; the first part gives the dimensions of the W section. The flange’s breadth is 7.50″, and the overall depth is 18 inches. The area is 14.70 inch2.
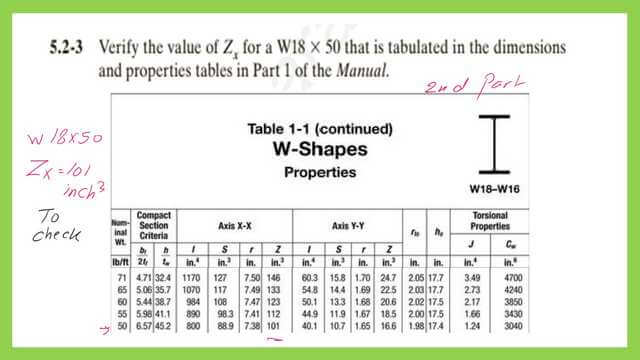
Find the Zx for W18x50 from Table 1-1.
In the next slide, we view the second part, which gives the value of Zx, 101.0 inch3. The same is the value estimated via Table 1-8. It matches our previous calculations as a two-weight section. The validation is okay.
Verify Zx of W18x50 by considering areas of flange and web.
If we consider the W section composed of areas, the first is the flange, which is 7.50″ by 0.57″.The second is the web, with a height of (18-2*0.57)= 16.86 inches. The last is the lower flange area, which is 7.50″x0.57″ inches.
The total area is equal to 14.535 inch2. Consider the plastic section modulus equal to Mp/Fy, which can be rewritten as C*yct/Fy=At/2*yct.
The area(At/2)=0.5*14.70=7.35 inch2. use the sum of areas*y distance and divide by At/2 to get the H-y bar distance.
The next slide shows that we get the (h-y )bar value, the distance from the point of application of At/2 top of the Plastic neutral axis, equal to 6.8622 inches, and the Zx value of 99.742 inches, less than 101.0 inch3.
The previous post is “6A-Practice problem 5-2-2 Find y bar, Zx, and Zy for the un-symmetric section.
For bending members, please refer to Chapter 8-A Beginner’s Guide to the Steel Construction Manual, 15th ed.
The following post is “6c-Practice problem 6-17-5-find Sx and ZX for W18x35.