Last Updated on October 1, 2024 by Maged kamel
Introduction to Macaulay’s function and Singularity functions.
Macaulay’s function and singularity function are essential concepts in mathematical analysis. Macaulay’s function is a mathematical tool that defines a piecewise function that combines polynomials with different degrees. On the other hand, the singularity function is a mathematical function commonly used to represent concentrated loads or forces in structural engineering. These functions play crucial roles in various areas of mathematics and engineering.
What is a step function?
There is a function called the unit step function or Heaviside function that starts after a certain time when we plot t as the x-axis and the Heaviside function as the Y-axis.
We can express the relation as H(t-a) equals zero for t is bigger or equal to zero and less than a but equals one unit when t >=a. It forms a step shape with an equal riser, which is extended for values of T >a.
The upper part of the slide shows a familiar line graph. When a line of positive slope m passes by a (0,0) point, its equation can be expressed as a y function equals y=mx.
If the same line was shifted by a distance a from the y-axis and maintained the same slope m, then y is expressed as y=m(x-a). But when the line is shifted by a distance a- from the y-axis and maintains a negative slope (-m), the equation can be expressed as y=-m(x-a).
We will utilize this expression later when dealing with a triangular load. But the y-axis will be w(x), and the load expression is written as w(x)=+w/b(x-a), where the base is the load base, and w is the ordinate load intensity.
The line can express a uniform load starting from a distance (a) from the left edge and extending to the end of a beam. Its equation will be W(x)=w(x-a)^0, where w is the intensity of the uniform load. We use the expression of w(x-a)^0 to include that the load at x<a is considered zero, while for values bigger than a, it equals w.
Represent the shear function for a beam as a group of step functions.
In the next slide, if we have a beam with length L having two supports and acted upon by a concentrated load at a distance a from the left support, the remaining distance to the right support is b.
We estimate that the reaction at the left support will equal (P*(b)/L. Meanwhile, the reaction at the right support will be equal to P*(a)/L.
To express the shear function, we can consider the previous beam as an assembly of three-step functions using a step function. The first case is the shear from the left reaction force, expressed as Q(x)=+P*b/L in the form of a step function with a rise equal to P*b/L extending to the end of the beam.
To express the load P as a shear function, it also acts as a step function starting from distance a, with a rise of -P and extends a distance (L-a). Finally, the right support reaction with a value of P*(a/L) is a step function starting from x=l with a shear value of -Pa/L. The previous shapes can be combined to form the shear diagram as shown.
In the next slide, I quote from Prof. Timothy Philpot’s book, An Integrated Learning System. Macaulay’s functions represent quantities that begin at point a.
Before point a, the function has a zero value.
After point a, the function has a value of f(x-a)^n, since a distance a. Macaulay’s function shifts it is expressed not by parentheses but with a different form, smaller than and bigger than signs or bracketed terms. The function value is 0 when x is smaller than a and (x-a)^n for x> or equal to a.
Macaulay’s function with different n values.
In the next slide, Macaulay‘s function deals with three values of n as n=0,1 and 2. When n=0, the function is a straight line, and the y value is (x-a)^0=1 when x=a or bigger than a and zero for x<a. that expresses a uniform load.
Macaulay function when n=1, the function is expressed as an inclined line, and the y value is (x-a)^1=1 when x=a or bigger than a and zero for x<a.
This function is a ramp function that expresses a linear load. The last form is when n=2, where< x-a>^2 expresses a parabolic plot. The parabolic plot can be used to explain the moment values of distributed loads acting on a beam.
Introduction to singularity functions.
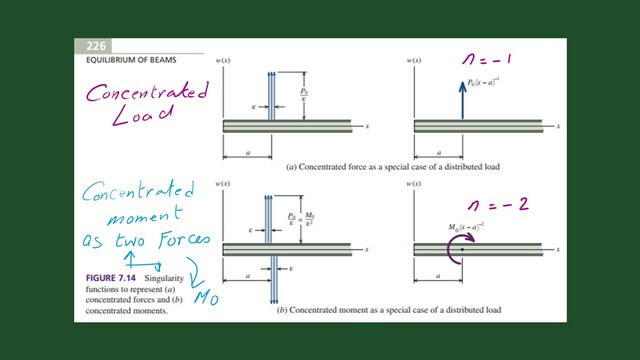
The next slide shows new singularity functions, where n =-1 or n=-2. These singularity functions can be used to express concentrated loads and moments.
These functions can give the value of the load intensity in case of a concentrated load P0 acting as w(x) as =P0*<x-a>^-1 as equal 0 when x does not equal a and equals P0 when x=a, in that case n=-1.
In the case of a concentrated Moment M0 acting, the load function expressed as w(x) as =M0*<x-a>^-2 equals 0 when x does not equal a and equals M0 when x=a. The n value equals =-2 in this case.
The first graph shows the relations between W(x) and P0*<x-a>^-1 function shifted by a distance a. While the second graph shows the relations between W(x) and M0*<x-a>^-2 function shifted by a distance a.
The difference between the integration of Macaulay’s function and the integration of the singularity functions.
In the case of Macaulay functions, where n >0, after integration, we add 1 to n and divide by (n+1), the same as any ordinary function. In the case of singularity functions. Where n<0, after integration, we add 1 to n, and there is no division by (n+1).
The difference of the integration between Macaulay’s function and discontinuity functions.
This is an introductory link to Macaulay’s function.
This is a link to my “