Last Updated on August 31, 2024 by Maged kamel

Practice problem 6-17-5-find Sx and ZX for W18x35.

Practice problem 6-17-5-find Sx and ZX for W18x35.

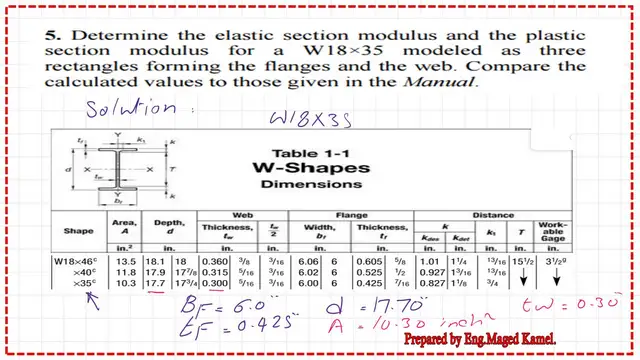
Determine the elastic and plastic section modulus for a W18×35 modeled as three rectangles forming the flanges and the web. Compare the calculated values to those given in the Manual. This practice problem is quoted from the Unified Design of Steel Structure Book.

We will use Table 1-1 to get the information for W18x35, which includes the flange width and thickness and the overall height and width of the web.

The sketch shows that the flange width is 5 inches, while the thickness is 0.425 inches. The web width is 0.30 inches, The total depth is 17.70 inches, and the area is 10.30 square inches.

Please refer to the next slide image for more details.

 

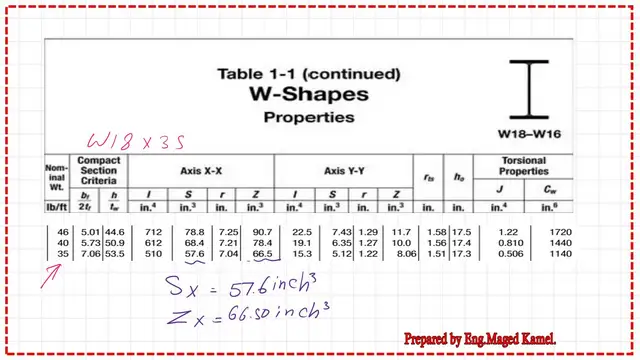
The value of elastic section modulus and plastic section modulus is shown in Table 1-1.

In the next slide, refer to part 2 of Table 1-1; the value of the elastic section modulus is 57.60 inch3, while the plastic section modulus zx is 66.50 inch3.

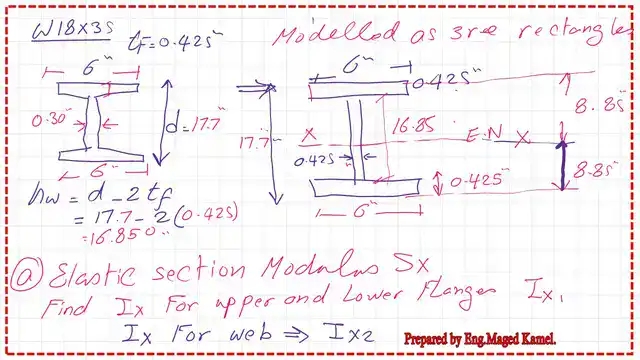
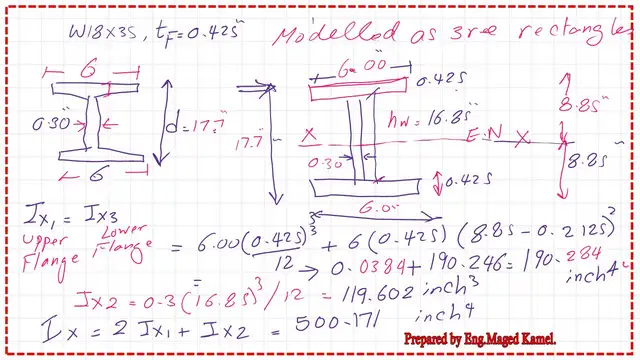
In the third slide, the section of W18x35 is drawn as an I shape with the different items explained for flange and web. Next to the W section is an assembly of three rectangles representing the section.

The upper rectangle, which has a width of 6 inches and a width of 0.425 inches, represents the upper flange. The second rectangle, the web part, has a height of 16.85 inches and a width of 0.425 inches. The last rectangle, which represents the lower flange, has similar dimensions to the first rectangle. We need to find the values of the moment of inertia for the Flanges and the web.

The value of the moment of inertia Ix of W18x35 by estimation.

The overall depth of the W section equals 17.70 inches, and due to symmetry, the elastic section modulus will pass by the middle portion of the W section.

The moment of inertia of the upper flange and the lower flange about the elastic section modulus is the same. It equals the Inertia about the cg of the flange plus the product of the flange area by the square of the distance from flange Cg to the elastic section modulus.

The moment of inertia of the upper flange to the neutral axis Ix1 equals 190.284 inch4. The moment of inertia of the web to the elastic neutral axis Ix2 equals the width by height^3/12, which is 119.60 inch4. The final moment of inertia of the three rectangles about the neutral axis equals 500.171 inch4.

 

The value of the elastic section modulus Sx for W18x50.

After we have estimated the moment of inertia, we need to find the value of Sx, the elastic section modulus, and the distance from the E.N axis to the top, which is 8.85 inches. Sx equals Ix/y, which is 500.171/8.85=56.52 inch3. The exact value for Sx from Table 1-1 equals 57.60 inch3.

 

Verify Zx of W18x35 by considering areas of flange and web.

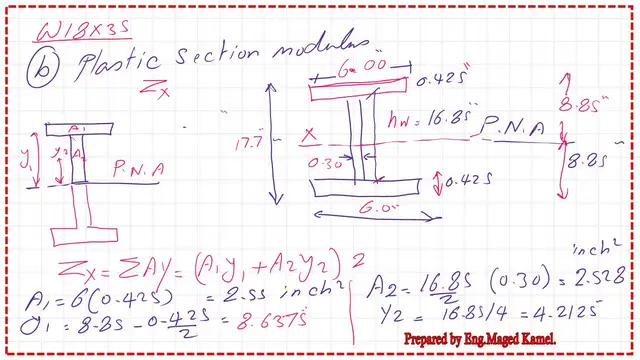
Again, we will use the three rectangles representing the W section to find the value of the plastic section modulus. The Plastic Neutral axis or P.N axis cuts the section in the middle due to symmetry. The Plastic section modulus Zx is the sum of Area products by the distance to the P.N axis.

We will consider the upper rectangle and half of the vertical rectangle. The upper rectangle area, A1, equals width by thickness, which is 6*0.425=2.5 inches. The perpendicular distance from Cg to the plastic axis is 8.85-0.5*0.425=8.6375 inches. The area of half of the web equals 0.5*16.85*0.30=2.528 inch2. The Cg distance to the P.N axis equals 19.85*0.25=4.1225 inch2.

Please refer to the next slide for more details.

 

The next slide shows the steps to get the Zx or the plastic section modulus for W18x35. By estimation, the Zx value equals 65.35 inch3, while the exact value for the plastic section modulus from Table 1-1 equals 66.50 inch3. We could use a quicker way to estimate Zx by considering the section as one big rectangle of b1=6 and d1=17.70 inches, and an inner rectangle of width equals 5.70 and depth d2=16.85 inches. Zx can be estimated as (b1*d1^2/4-b2*d2^2/4), which equals 65.345 inch3. Thank You.

The previous post is 6b-Practice problem 5-2-3-verify Zx for W18x50.

The following post is 6d-Practice problem 6-17-11-find Sx and ZX for WT5x22.50.

For bending members, please refer to Chapter 8-A Beginner’s Guide to the Steel Construction Manual, 15^th ed.

A newly added post, 6d-Practice problem 6-17-11-find Sx and ZX for WT5x22.50.