Last Updated on June 23, 2025 by Maged kamel
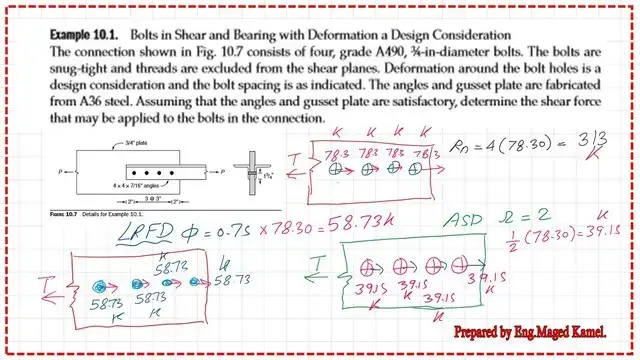
Solved problem 10-1- how to get Bearing value-ASD-3-3.

This sketch compares the LRFD and ASD values of nominal bearing loads, as well as the total values for each. The upper limit criteria is (2.4*db*tp*Fu); The thickness of the plate is termed tp=3/4″; the bolt diameter db=3/4 inches. The ultimate stress of A36 plate is Fu=58 ksi, then the product 2.4db*tp*Fu=2.4(3/4″)(3/4)(58)=78.30 kips.
The upper limit has controlled the design. As we can see, the value of the bearing based on the ASD for each bolt is equal to 39.15 kips; this value was obtained from the previous post. The next step is to verify these values by using both tables 7-4 and 7-5 for the bearing value-ASD values.
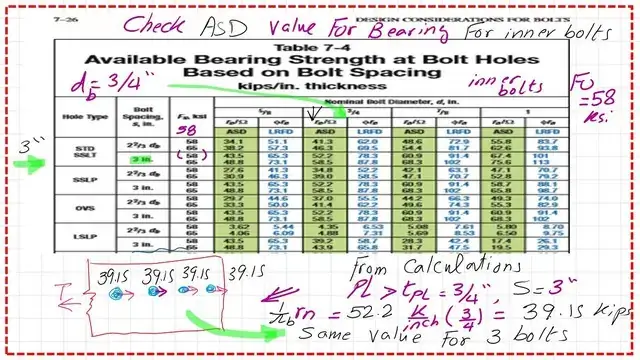
Using Table 7-4 for the Bearing value-ASD for the inner bolts.
For our solved problem 10- 1, to get the Bearing value based on the ASD design for the inner bolts. The bolt diameter is 3/4″, so we use Table 7-4 for determining the bearing values for inner bolts.. We have a group B for ASTM A-490. Then, by intersecting a row and the relevant column, we obtain the value of Rnb.
From Table 7-4, for the ASD value, for the solved problem 10-1 we have inner spacing 3″ and Fu=58 ksi, 3/4″ plate thickness, the selected value is 52.2 kips/inch, since the value is per inch we will multiply by the value of the plate thickness which is 3/4″ and multiply by the number of inner bolts n=3. The final value for intermediate spacing of 3″, Rn/Ω=52.2 *3/4*n =52.2*3/4*3=117.45 kips.
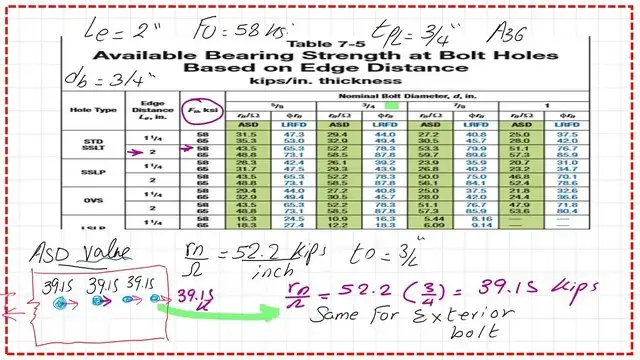
Using Table 7-5 for the Bearing value-ASD for the external bolts.
For the solved problem 10-1, we proceed to table 3-5 for the external bolt bearing value. Estimate the bearing value -ASD for the edge distance 2″, Fu=58 ksi, and from the column of 3/4″ for bolt diameter.
We calculate the force value at the intersection as 52.2 kips/inch. We then multiply this value by (3/4), which is the plate thickness, and multiply by n=1, since we have one external bolt. The value of Rn/Ω is 39.15 kips.
The sum of all the bearing values of all the bolts can be finalized as Rn/Ω = 117.45 + 39.15 = 156.60 kips. Verify the ASD value from the previous calculation using the same equation; the calculations yield the same value.
For the solved problem 10-1.The final selected value of the shear force that is to be applied.
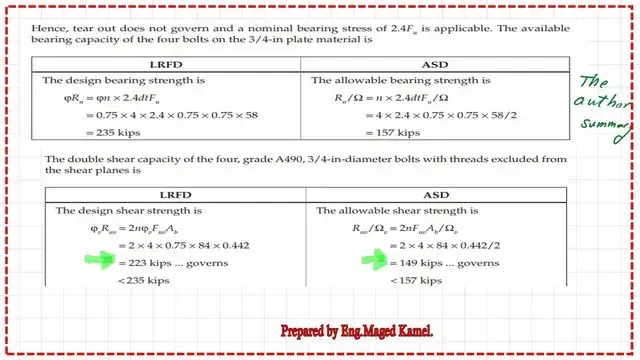
The final step is to select the minimum value of the nominal shear strength and the bearing nominal strength. For the shear nominal value, LRFD=223 kips, and ASD value=149 kips. Bearing strength for LRFD equals 235 kips, and for ASD equals 157 kips.
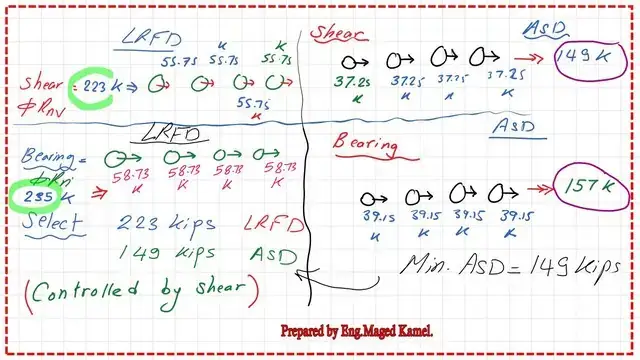
The lowest number is 223 kips, and ASD = 149 kips, since when the load value reaches 223 kips, according to LRFD, a failure will occur due to bearing.
This is the criterion for selection. We have reached the end of this solved problem 10-1 – The last part. Thank You.
The complete data, as estimated by the author, and the relevant tables for shear and bearing are included in the next slide image. The calculations are similar to our estimated calculations for shear and bearing values for the given connection.
This is a beneficial source for the design of various Steel elements, A Beginner’s Guide to the Steel Construction Manual, 15th ed, Chapter 4 – Bolted Connections.
This is a link to the first part of the same solved problem.
This is a link to the second part of the solved problem.
The next post is A solved for bearing connections.