Last Updated on September 17, 2026 by Maged kamel
- A solved problem 10-1-for bearing connection-1-3
- A solved problem for a bearing connection: How to get the Value of Shear for a bearing connection?
- Solved Problem 10-1: the first method to get Shear strength for a connection using Table J3.2.
- Solved problem 10-1 for a bearing connection: the second method is to get the Shear strength for a connection by using Table 7-1.
A solved problem 10-1-for bearing connection-1-3
A solved problem for a bearing connection: How to get the Value of Shear for a bearing connection?
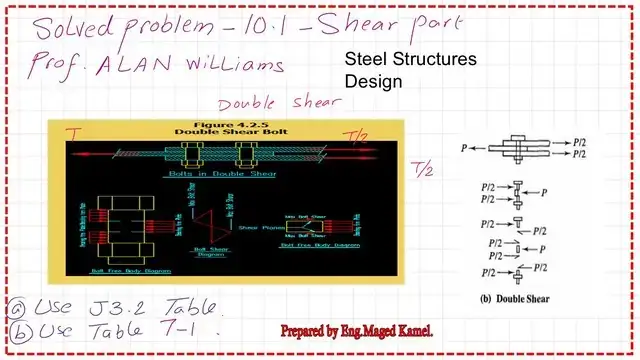
We will review problem 10-1, specifically the Shear part, from Prof. Alan Williams’s book. The first part will estimate the Shear force applied to a connection based on Bolt Shear. This is a double-shear case. I have included a sketch illustrating the Shear force distribution for double Shear, as quoted from the Engineering Beginner site.
We will start by checking the solved problem 10-1. The title is ‘Bolts in Shear and Bearing with Deformation: A Design Consideration.’ So, the item that we are dealing with is the 0.25″ deformation.
Figure 10.7 illustrates the connection, which features a double-angle connection with a gusset plate. The two angles are back-to-back, with a gusset plate; each angle is 4x4x with 7/16″ thickness.
The guest plate is 3/4″ thick and consists of four A490-grade 3/4″- diameter bolts. We have four grade A490, Which are type B.3/4″ diameter bolts, with snug-tight, for which bolts are tightened by a spanner, and no pre-tension is done.
The threads are excluded; then the connection is Type B and Type X from the Shear planes. Deformation around the Bolt is a design criterion, and the Bolt spacing is as indicated: the inner Bolt spacing is 3″, and the edge distance is 2″.
Assuming that the angles and gusset plate are satisfactory. As I understand it, there is no need to check the angle under tension against bearing calculations for Bolt spacing and diameter.
The only requirement is to determine the S bolts’ Shear and bearing capacities. We will start with the Shear stress. The first step is to determine the Area of one Bolt with a diameter of 3/4 inch, Grade A490-X. The Area is 0.442 in².
Solved Problem 10-1: the first method to get Shear strength for a connection using Table J3.2.
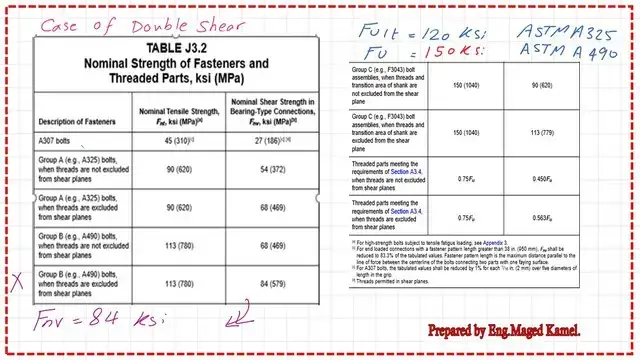
We have two methods to evaluate the nominal Shear strength; the first is to use Table J3.2. The next slide shows the AISC-360-16 provision for the equation used to get the Nominal Shear Value.
We have Table J.3.2 for the A solved problem 10-1-forbearing connection, which we included in the last video. Let us review our given data. We have bolts classified as group B per ASTM A490 and Are Excluded.
Then multiply ( Fnv) by the number of bolts and the Area of each Bolt. We get Rnv = 297.02 kips. To get the design nominal Shear strength, multiply by the phi Value, which is 0.75. The LRFD Value of Shear strength is 222.8 kips.
For the ASD Shear strength Value, multiply Rnv by (1/ omega). The omega Value is 2. The ASD Value is 148.152 kips. Please refer to the image on the next slide for more details.
Our case is the fourth item in the table. We have the highest nominal Shear Value of 84 ksi. This Value is for single Shear; we will multiply it by 2 for double Shear.
Solved problem 10-1 for a bearing connection: the second method is to get the Shear strength for a connection by using Table 7-1.
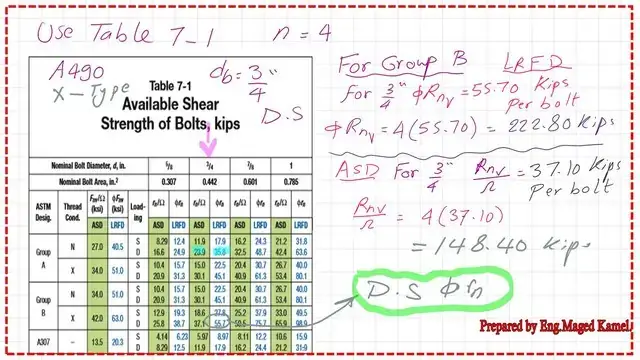
Table 7-1 gives the Shear Fnv Value for both LRFD and ASD, based on Bolt diameter. For Problem 10-1, we have a 3/4-inch Bolt, Group B, Type-x.
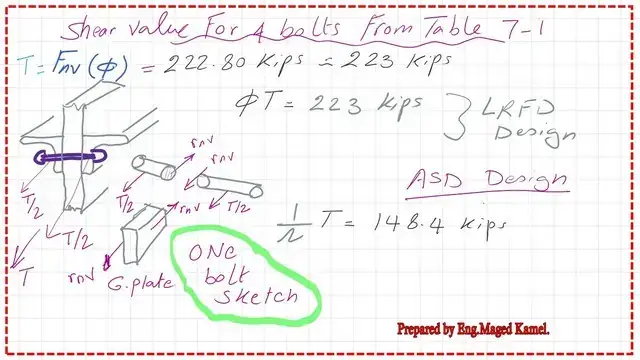
The φ*Rnv for a double-shear Bolt is 55.70 kips per Bolt, which we will multiply by the number of bolts(4).) The design Shear strength is 222.80 kips, which matches the previous estimate from Table J3-2.
The (1/ω)*Rn_vv for a double-shear Bolt is 37.10 kips per Bolt, which we will multiply by the number of Bolt 4 (4The ASD design Shear strength is 148.40 kips, which matches the previous estimate from Table J3-2.
A sketch shows the Shear force distribution for both LRFD and ASD design values. The Shear force acts opposite to the applied force.
The figures shown are the Shear values for the connection in solved problem 10-1, as quoted from the author’s book.
This is the PDF file for this Post, which you can view or download using the button below.
You can buy the PDF for solved problem 10-1, which combines posts 5, 6, and 6a, for just three dollars via this Link.
This is a very useful source for designing various Steel elements: A Beginner’s Guide to the Steel Construction Manual, 15th ed, ..Chapter 4 – Bolted Connections.
This is a very useful source for designing various Steel elements: A Beginner’s Guide to the Steel Construction Manual, 16th ed., Chapter 4 – Bolted Connections.
The next Post, Post 6, is solved problem 10- 1: how to get bearing Value- LRFD-2-3