Last Updated on April 27, 2024 by Maged kamel
Definition of the effective area for tension members.
Effective area and shear lag factor.
To explain the concept of effective area, let us check that the shape, as shown in the sketch, is an angle under force tension force P with bolts at the lower leg.
The shaded area is stressed very little, which means that most of the stresses occur at the bolts located at the lower leg. And connected to the plate.
As the load is applied, the transfer of that load to the unbolted portion, will not occur immediately but, after a lag, that is why this phenomenon is called shear lag.
Note that the angle is connected alone with only one leg, and only one leg is connected to the plate. This leads to a concentration of stress along that leg and leaves a part of the unconnected leg part of the un-connected leg unstressed or stressed very little.

This means that stress for the connected portion will be increased due to the lack of sharing of the unconnected part, which may exceed the Fy. The further we move out from the connection, the more uniform the stress becomes.
In the transition region, the shear transfer has lagged, a phenomenon known as shear lag.
This leads to deriving an expression to measure the percentage of effective area to the net area, which is called the U. The U value depends on two factors. The first factor is the x̅ bar which is the distance from the Cg to the connecting plate. factor. the second factor is the connection length L.
Effect of x̅ and connection length on the shear lag factor.
Comparing two shapes, shape a with an equal angle and shape b with an unequal angle, where the fasteners exist on the long leg side, the observation is that when the distance x̅ is smaller, the effectiveness of the connection improves. The smaller the value of x̅, the larger the effective areas of the member and, thus, the larger the member’s strength.

The x̅ is closer since the bigger area has a closer CG, as known from the statistics. So the angle in shape b is more effective than in shape a. Shear lag affects both bolted and welded connections, therefore the effective net area concept is applied to both types of connections, then Ae=U *An, and also for welded connections.
Does the shear lag factor U have a minimum value?
The U shear lag factor U has a minimum value specified by The AISC, which is the ratio of the connected area to the total area; this holds true for open areas. The Code has identified the shapes under tension force to open shapes such as W, M, S, HP C, and their related structural shapes and angles.

Table D3.1 shows the shear lag factor for CM-14 and its related specs.
Case-1 is the first case for which the U value equals 1; this case includes the connection of two steel shapes that are fully connected together. For instance, if we have two W shapes or two channels connected at flanges and webs. or completely welded.
Case 2 is the second case for which the U value is less than 1, and we need to find the two parameters x̅ and the connection length L.
This case includes connecting two steel shapes that are not fully connected. For instance, two W shapes or two channels connected only at flanges, through webs, or partially welded.
Case 3 is the case where the two connected shapes are connected through transverse welds, for instance, two plates or two angles through one leg for each. The U value is equal to 1.
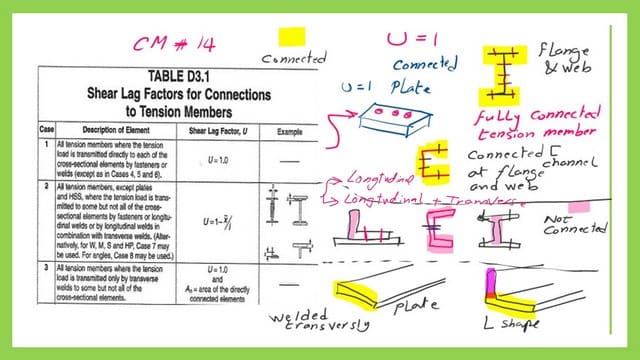
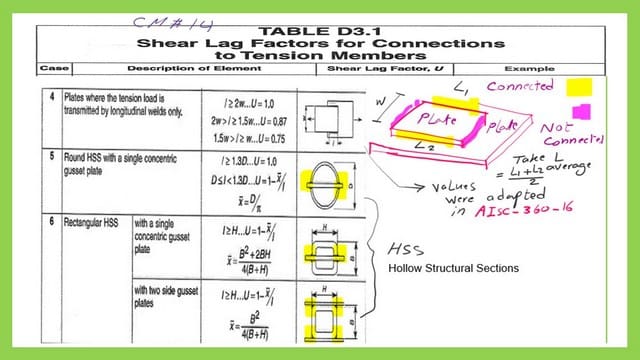
Case 4 is where the two connected plates are connected through two longitudinal welds, for instance, two plates. The U value depends on the width of the connection. There are three values of U based on the ratio between W and L. The length of connection L is the average length of the two longitudinal lengths.
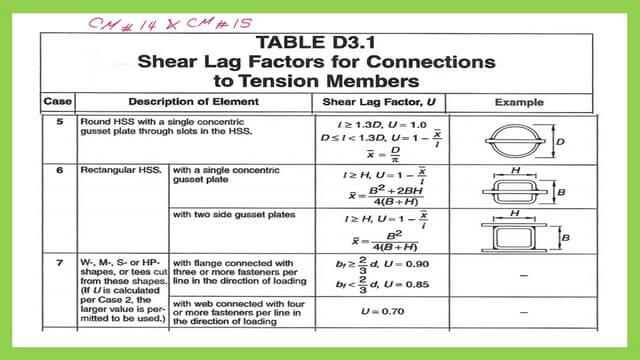
Case 5 is a round HSS with a single concentric plate, and case 6 is a rectangular HSS with a single concentric plate or two side gusset plates.
Shear lag factor as per CM#15 and related AISC-360-16.
The value of U for case 1 for table D3.1 as per CM#15 is the same as case 1 for table D3.1 as per CM#14
The major difference between Table D3.1 in AISC-360-16 and Table D3.1-AISC-360-2010 is between cases 2 and 4.
For CM#15, case 2 was revised to include connected members through longitudinal welds in combination with transverse welds.
For CM#15, case 4 was revised to case 4a, which includes plates, angles, Tees, W shapes, and channels through longitudinal welds only. The u equation has been revised.

Common values for U for cases 5-8 between CM#14 and CM#15.
For Cases 5-8 in Table D.31, shear lag factors, there is no change between CM#14 and CM#15. Case 7 includes W,m, S, Hp, or shapes cut from W,m, and Tees.
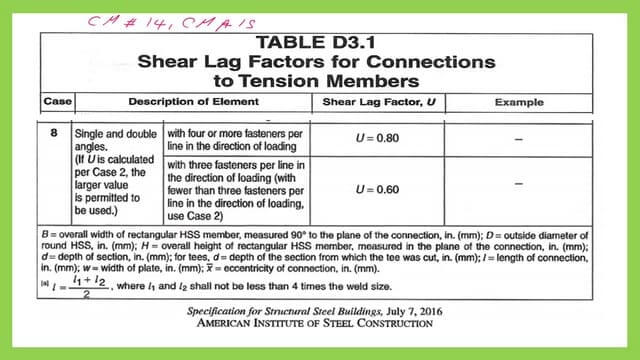
Case 8 is the case of a single or double angle connected through bolts; the value of u depends on whether the connection is with four or more bolts or with three or fewer bolts.
Solved example 4-1: How can we estimate the shear lag factor for a single angle?
It is required to determine the shear lag factor U, the net area An, and the effective area Ae. We have an angle of 5x5x3/8 inch, with 4 bolts connected to one plate from one side.
We want to estimate the value of U. Bolts, which are four 3/4-inch A325 N bolts, so we can estimate the hole diameter by adding 1/8 inch to the bolt diameter.
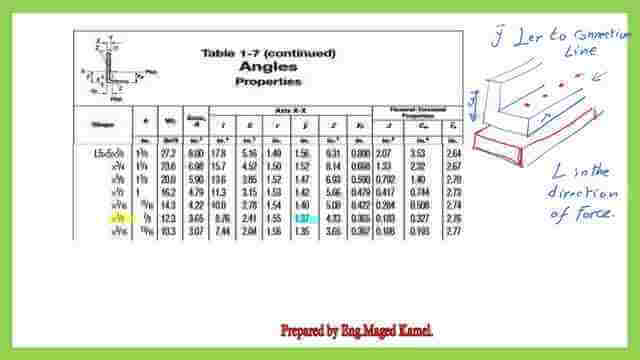
The hole’s diameter is 7/8 inch. Our expression U=1- x̅/ L, where x̅ is the distance perpendicular to the load. Refer to the table. Then, we get the gross area for angle 5x5x 3/8 inch, which is 3.65 inch2.
Check the CG distance. The C.G. is in the y-direction, but it is referenced as x̅ and equal to 1.37 inches. What about the L distance? It is the distance between the first bolt and the last bolt, which is equal to (3*3=9 inches), so U=1-(1.37/9)=0.848.
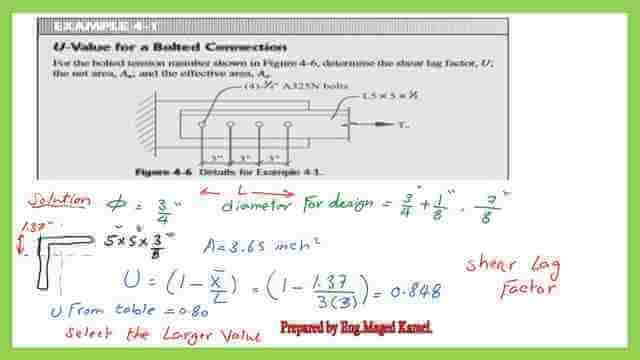
This is the calculation for the U value, but if we refer to the table, U=0.80 for four or more fasteners, as in the third case of the table, as shown.

We select the bigger of the two values, 0.848, and then estimate the net area using the usual equation: Anet=Ag-(n*dh*tl).
We can get the y bar for the angle L5xL5x 3/8 from Table 1-7. y bar. We can see that the y bar is parallel to the unconnected leg.
The net area Anet=Ag -Ag- sum(d*t), Ag =3.65 inch2, dia 7/8 and t=3/8 of the angle, sum(d*t)=7/8*3/8, only one bolt hole to be deducted, to be deducted from 3.65 inch2.
The value is 3.32 inch 2, then A -effective=0.848*3.32=2.82 inch2, which was the first example of the effective area.

This quick reference to posts that include practice problems for U value.
A) Design strength for a given W section bolted at flanges; this is the topic of the next post; it is a direct application for cases 2 and 7 for shear lag factor. The next post-post 7- is A Solved problem for Design strength.
B) For the shear lag factor U value for a welded angle, which applies to case 2, please refer to post 8.
C) For a connected angle by bolts for one leg only, the value of U is governed by the maximum value between case 2 and case 8. Please refer to the first solved problem in post 9.
D) For a connected section by transverse weld only in case 3, please refer to the post-9A-Practice problem-transverse weld of a WT section.
E) For a connected section by longitudinal weld only in case 4, please refer to the post-9b-Practice problem-longitudinal weld of a plate section.
F) For a connected section by longitudinal weld only, case 4, please refer to the post-9C-Practice problem-longitudinal weld of a C section.
For the same angle welded, the value of U is governed by case 2; please refer to the second solved example in post 9.
Chapter 3 – Tension Members– A Beginner’s Guide to Structural Engineering is a great external resource.

