Practice problem-transverse weld of a WT section.
This is a Practice problem for the Transverse weld of a WT section, this is case 3 for the shear lag factor table D3.1.
A given WT5x15 section Of A922 steel with transverse weld to its flange as shown in Figure P3-32 is required to find The LRFD and ASD values neglecting the block shear.
Estimate the minimum value of shear lag factor U.
1-From the given Data for the ASTM A992, we can get the yield stress Fy=50 ksi and the ultimate stress Fult as equal to 65 ksi.
2- From the given section of WT5x15, we can find the following data. The first item is the area of the given section, the area will be equal to 4.42 inch2.
The breadth of the flange is bf=5.81 inches, and the width of the flange equals 0.51 inches. As for the overall depth, it will be equal to 5.24 inches and the width of the stem is 0.30 inches.
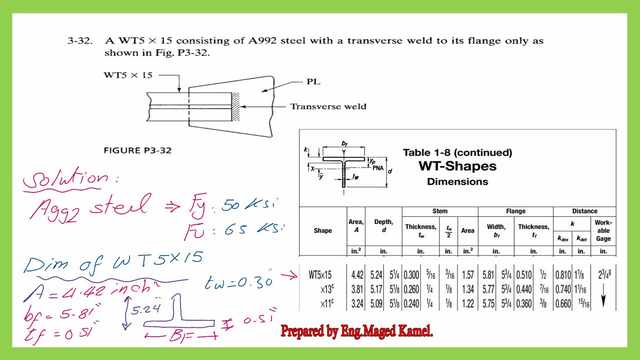

3- The minimum value of the shear lag factor U can be estimated as the ratio of the connected area by the transverse weld over the total area of the Wt section.
4- The connected area is equal to the width of the flange by its thickness, which is the product of 5.81*0.51=2.9631 inch2.
5- The U value equals the connected area over the area of the section or equal to 2.9631/4.42)=0.67.
The estimation of the effective area.
The flange part is connected to the guest plate but not all the Wt section and the connection is done through a transverse weld only.
6-To get the effective area, multiply the value of U which is equal to one by the connected area which is equal to 2.963 inch2. The next slide image shows the details of Table D3.1 based on #2010 specs case 3.


The same estimations match with CM#15 and 2016 specification, same case 3 is also marked.


The next slide image shows the equations used for the estimation of the factored nominal strength for the tensile yielding and Tensile rupture.


Nominal strength for Practice problem-transverse weld of a WT section.
We have two cases for the nominal strength, the first case is the case of tensile yielding for which we consider the area as the full area and the tensile strength is equal to yield stress multiplied by the area and can be found as (4.42*50)=221 kips.
The second case for tensile strength is the case of rupture strength in which the value is found to be equal to the effective area multiplied by the ultimate stress. and can be found as (2.963*65)=192.6 kips.
The U value explained for Case -3 as All tension members where the tension load is transmitted only by transverse welds to some but not all of the cross-sectional elements.
LRFD strength for Practice problem-transverse weld of a WT section.
Multiply the first value of the strength due to yield by the reduction value of PHi equal to 0 .90, we can get the LRFD strength due to yielding as equals 199 kips.
Multiply the second value of the strength due to rupture by the reduction value of PHi equal to 0 .75, we can get the LRFD strength due to rupture as equals 144 kips.
We will select the lesser value as our final LRFD strength which equals 144 kips, this is an indication that the LRFD strength is governed by rupture.


ASD strength for Practice problem-transverse weld of a WT section.
Multiply the first value of the strength due to yield by the reduction value (1/omega) equal to (1/1.67), we can get the ASD strength due to yielding as equals 132.33 kips.
Multiply the second value of the strength due to rupture by the reduction value of (1/omega) equal to (1/2), and we can get the ASD strength due to rupture as equals 96.30 kips.
We will select the lesser value as our final ASD strength which equals 96.30 kips, this is an indication that the ASD strength is governed by rupture.


The next post is 9b– Practice problem-longitudinal weld of a plate section.
Chapter 3 – Tension Members– A Beginner’s Guide to Structural Engineering is a great external resource.

