Two Solved problems for an estimate of effective net area.
This is the brief content of the lecture.


Solved problems for determining the U value for different shapes.
Refer to shapes as per Figure 3.10 from Prof. Segui’s handbook. He makes examples of the different shapes, and their u values, for example for single or double angles with two or more fasteners.
We will have different shear lag factors, this is derived from the table for the single angle, or double angles, when the angle is connected to a plate, for which we have two different U values if we have at each line three or more fasteners, then U =0.80.
But if two or three fasteners then U=0.60. Please refer to item #8.
The first figure is for two or three fasteners. The next shape is for four fasteners and more than U=0.80, for W sections, he gave different sections.
For example w10x19 the w section is bolted at both the upper and lower flange with four bolts, then u=0.85, if we refer to the table for w sections, and write the breadth of flange bf=4.02 inch and overall depth =10.2 ” and overall depth =10.2 ”.
Estimate the bf/d, If bf/d>2/3, then U=0.90, but if bf/d<2/3, then U=0.85, for the case of w10x19, we have bf/d is =0.394 <2/3 then U=0.85 this rule is from the table. Please refer to item #7.
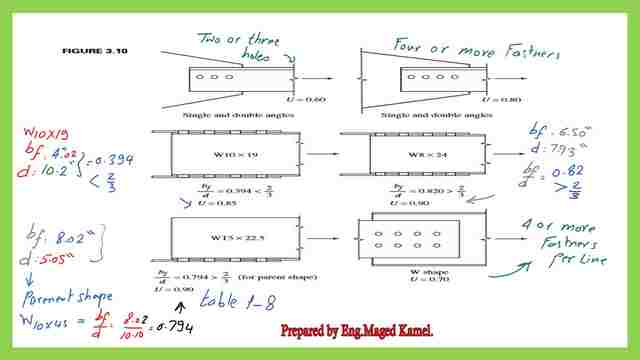

For W, M, S, or Hp shapes, having bolts at the top and bottom flanges With three or more fasteners, this is the rule if the bf > 2/3*d, 0r bf/d=2/3 then U=0.90, but if the bf< 2/3*d, then U=0.85.
For the w section, if for w 10x 19 the upper flange has 4 bolts at the top and bottom, bf/d=0.394< 2/3 then U=0.85, for the other case with w8x24, the depth of the beam is small, the beam is shallow, d is 7.93 ”, if we divide bf/d we get 0.82> 2/3, then U=0.90, this is the case in the table for w section.
If we have Wt, which means it is a T shape, cut from a W section, if we refer to the property for wt 5x 22.5 from the table we have the bf=8.02″ and d=5″ if we divide bf/d=8.02/5.05, we will find that the ratio will be >1.
What is the parent section? The parent section is W10x45. the depth is twice the Wt section, then bf/d=8.02/10.1=0.794, then the U value =0.90.
In the last case if we have a W shape bolted with two lines of two lines with 4 or more fasteners per single line but these fasteners are at the web, this is the case shown in the table, the U value is =0.70.
The next tables for the u value are enclosed for quick reference to match with the examples given by Prof. Segui which are presented in the previous slide image.


The next table shows case Number 3 in the specification.


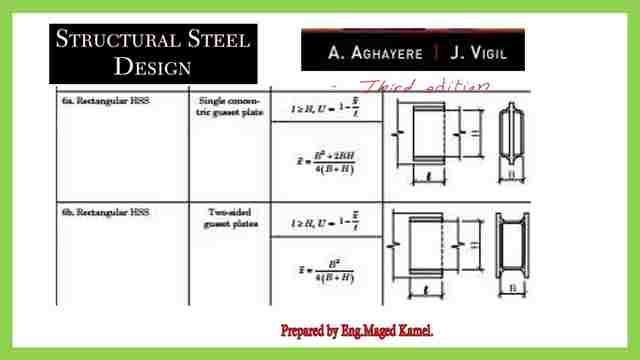
Case 6a and 6b, for a rectangular Hss, welded to a gusset plate in the middle.

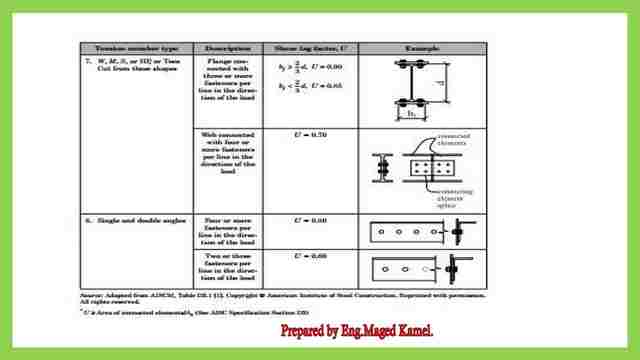
The table shows cases 7&8 for tension members.

The first solved problem 3-4 of the two solved problems for an estimate of effective net area.
In the first solved problem-3-4 Determine the effective net area for the tension member in Figure 3-12, the given angle is 6×6 x1/2″, and I put the corresponding u value for the angle with fasteners.


If we refer to table 1-7 for the angle 6x6x1/2″, for the solved problem 3-4, we will have y̅ value is 1.67″, which will be considered as x̅ the vertical distance to the connection line or the force line. We need to estimate the net area and U factor, then multiply to get the effective net area.
We have two lines of bolts and each line has 3 bolts, each bolt dia is 5/8″, we add 1/8″ then the d hole=6/8″, for the net area determination, the sum of d *t, where t is the leg thickness, where t is the leg thickness, which 1/2.then Area net=2*(6/8)*(1/2)=6/8 inch2, This is deduction value from the Area gross.
In the next step, The u value to be estimated from case 2-U=(1-x̅/L), L is the length, for x̅ we have obtained from the table, while the L value is from the first fastener, bolt, to the last one which is=3*2=6″, then U= (1-(1.67/6)) =0.7217. this value is greater than the U estimated from Case 8, which is equal to 0.60.
Our gross area value is 5.77 inch2, we will deduct (6/8) inch2, then the net area equals 5.02 inch2.
To get the effective area we multiply the net area by the shear lag factor U, which is equal to 0.7217.
The A-ffective=5.03*0.7217=3.623 inch2.


The second problem 3-5 of the two solved problems.
Referring to solved problem 3-5, if the tension member-single angle of problem 3-4 is welded as shown in fig 3-13, determine the effective area, from the last time, A effective was= 3.623 inch2.
The same equation for the U value is used with the same x̅ but this length, average length of welds, for 1/2(5.5+5.5)=5.5 “, U=1-(1.67/5.5)=0.696, but since no deduction due to bolts, the Anet=A gross, then the area effective Aeff=U*Anet=U*A-gross.
The value of the effective area, A eff=5.77*0.696=4.02 inch2. rupture tensile value, in this case, will be more than the case of bolts since A effective is bigger.


This is the pdf file used in the illustration of this post.
The next post is For a connected section by transverse weld only which is case 3, please refer to post-9A-Practice problem-transverse weld of a WT section
This is the post that represents the introduction to block shear, the Introduction to block shear.
Chapter 3 – Tension Members– A Beginner’s Guide to Structural Engineering is a great external resource.

