8- Easy Illustration of the Arithmetic Gradient.

Last Updated on January 24, 2026 by Maged kamel

Illustration of the Arithmetic Gradient.

The discussion will be about the Arithmetic gradient.

Our new subject for discussion will be the arithmetic gradient, but we will review the relationship between P and F, P is the present- value, and F is the future value. 

Review of the different types of investments.

Deposit money to get the retirement amount at the end of your investment (P/F) relation.

If you deposit money in a bank for the investment of an amount P, at a compound interest rate i%, you will receive a future F-value for your investment F.

We will find that we have different signs. P is represented by a downward arrow, or minus sign, since it is a cash-out, but when you receive an F value, it will be cash-in, and the value is drawn by an upward arrow. The P-value in terms of F, i%, n, and F in terms of P, i%, and n are shown in the slide.

  For the P-value,  it is P=F*(P/F, i%, n). For F- value it is=F=P*(1+i)^n. P- value= F* (1+i) ^-n. The relation is based on annual compound interest i%, but if we change the annual interest to quarterly compounding. The new interest rate i2=(i1/4%) and raised to the power of 4*(number of years), or 4n. That was the relation of F with a given P, I, and n.

Deposit money to buy a car at the end of your investment (P/F) relation.

There is another relation; for instance, if someone wishes to buy a car, they take a loan from a bank with an interest rate of i% and payment F will be made at the end of time n, this is from the bank’s point of view.

Cash in will be denoted by a plus sign (+), and the money received F will be cash out, denoted by a negative sign (-).

There is another type of relationship in which someone receives money to buy goods and pays it back through an instalment or a uniform series of compound interest after one year of receiving the cash, for the agreed-upon period. The P-value is cash in or with a positive sign.

The cash out with equal amounts will be cash out with negative signs; its value = A. The value for A in terms of P, i, n, A=iP(1+i)^n/((1+i)^n-1)), where i is the interest rate, and n is the time in years. The values of A are equal, the same as a uniformly distributed load with A value as cash in instalments in n the bank account, with an interest I and for some time.

Deposit money in a uniform series to receive insured money at the end of an investment (A/F) relationship.

For instance, if somebody wants to receive insured money after some time, he will pay equal instalments of value  A with an interest rate of i% and for n time, starting after one year, the diagram shows this type, the A values are shown as upward cash flow and at the end of time, for instance, time=8 years. The F- value received at the end of year 8, can be estimated based on a compound interest i%, the F- value= A(F/A, i%, n), also F=A/i((1+i)^n-1).

The arithmetic gradient factors.

We will discuss a new subject, which is the arithmetic gradient factors.
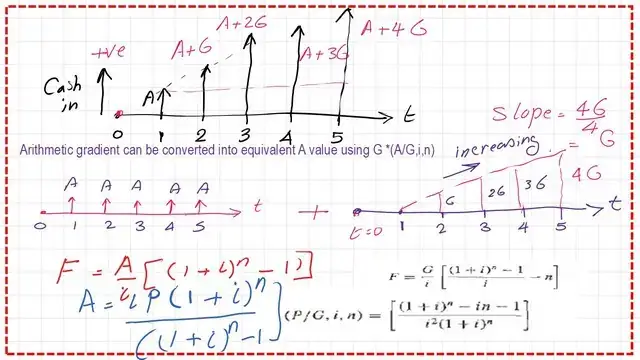
While paying instalments, these instalments are not of equal value, but the difference between each consecutive payment is constant and equals G, which is the same difference between the second and third instalments, also between the third and fourth instalments, as well as between the fourth and fifth instalments.

After one year of the agreement, someone pays an instalment of value A. The cash-in diagram has a shape of a trapezium shape, for which the smaller value is A and the larger base=A+4G  for the sketch shown where n=5 years. But if we have n years, the larger base value of the trapezium will be A+(n-1)G. But if we have n years, the larger base value will be A + (n-1)*G.

The previous shape is a trapezium, which can be solved by splitting it into two shapes.

The first shape is an equal instalment diagram with a cash-in value of A for 5 years.
The second part is a triangle with an increasing hypotenuse from 0 to 4G over 5 years, as shown in the sketch, with a slope of 4G/4 = G.
If we want to estimate the future value in terms of A, i%, and n. The relation is F=(A/i)*((1+i)^n-1)). If we want to estimate A in terms of P, i, n, the relation is F=(i*P)*(1+i)^n/((1+i)^n-1).

While for the triangular shape, the value for F is in terms of i%, n, G. F=(G/I)*(1+i)^n-1)/I)-n. P/G Find P in terms of G. The( P/G, i,n) has a relation, which is shown in the slide.

The PDF for this post can be viewed or downloaded from the attachment below.

External resource in Engineering Economy. This link illustrates different types of economies and how to make economic decisions—the time value of money, A good referance

The two coming posts are “What is Capital Recovery in the Economy?” and “A Solved Problem for EAW/ Equivalent Annual Worth.”

The third post: Arithmetic Gradient-part 2. How do you find P with the given I%,n, and G?