Last Updated on March 21, 2024 by Maged kamel
Uniform series of compound interest-1/2.
The content of the lecture.
The subject will be the uniform series of compound interest formulas and the uniform series sinking fund accompanied by solved problems
.

The present value P in terms of A, the uniform series of compound interest with I,n.
The first form is the relation between the uniform series and the present value. And how to convert from A to P and vice versa.
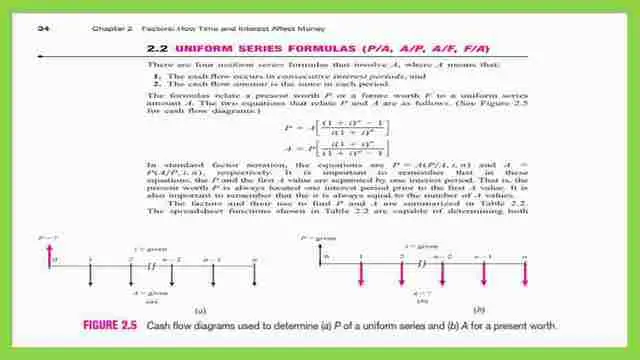
The Future value F in terms of A, the uniform series of compound interest with I,n.
The second form is the relation between the uniform series and the future value. And how to convert from A to F and vice versa.

Two cases are given, the first case is how to get F the future value when the interest I, A installment, uniform series, time in years, and n are given. The second case is how to get A the uniform series when the interest I, F, Future value, time in years, n is given.
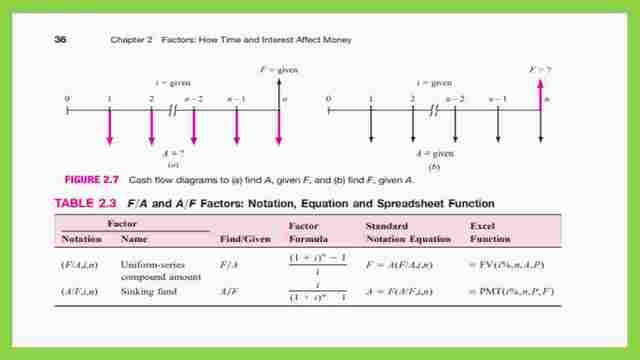
Equations for the relation between F &A.

How to derive the relation between A&F with given i,t?
The figure in front of you is a line representing time, divided into eight equal parts. The time scale starts at 0, which represents the time now. The figures from 1 to 8, represent the first year till the 8th year.
The arrows represent equal installments or deposits, with a constant value=A. These deposits are called uniform series of compound interest. The Uniform series of compound interest is from year 1 to year 8, it is required to estimate the Final money that will be obtained, which is denoted by the symbol F, at the end of Year 8.
The time scale starts at 0, which represents the time now. The figures from 1 to 8, represent the first year till the 8th year. The arrows represent equal installments or deposits, with a constant value=A.
These deposits are called uniform series of compound interest. This value is the final value due to the investments of the equal uniform series based on the I interest rate, which is considered annual interest.
We have a relation between the future value F and the present value P, which states that F=P*(1+i)^n, for the series of investments.
The F future value will be estimated as the summation of F values for a series of investments, for the first investment, A is invested for seven years which is the difference between time 8 and time 1.
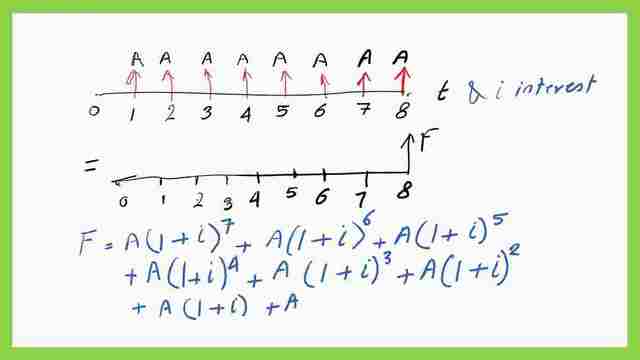
The future value F1=A*(1+i)^7, for the second investment starting at time t=2, we will add P*(1+i)^6, the n is =(8-2)=6. We have a total of 8 A, uniform series, the last investment has a time n=0, its future value F8=A*(1+i)^0=A. The next slide shows the final form of F or the future value for all of the investments.
We will multiply F by(1+i), and the right-hand side will be multiplied by (1+i).
F(1+i)=A*(1+i)^8+.A*(1+i)^7+A*(1+i)^6+A*(1+i)^5+A*(1+i)^4+A*(1+i)^3+A*(1+i)^2+ A*(1+i)^1.
Deduct the value of F from F(1+i). We will subtract the two equations, we will have similar items with different signs that cancel each other, and finally, we have i*F=A*(1+i)^8-A can be further put in a general form i*F=A*((1+i)^n-1)).
Try to substitute n=8 to check the previous expression. To check when n=0, iF=((A, where A is the amount of installment each year, multiplied by(1+i)^0-1)), we will have iF=AI, we will have iF=A*i or F=A.
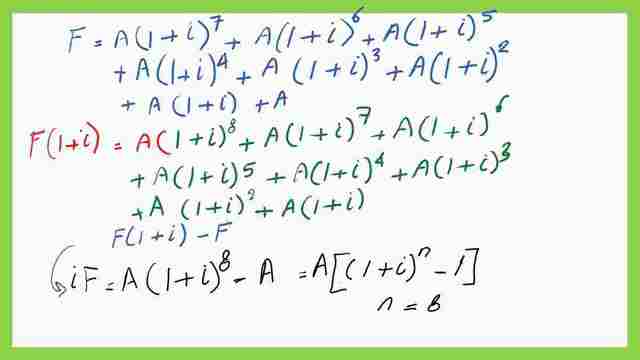
The expression used to get F in terms of A, i,n.
If we wish to write by using Symbols, then F=A*(F/A,i%,n), for the A written in symbolic form A=F*(A/F,i%, n), where i is the annual interest rate and n is the number of years. A=F*i/((1+i)^n-1).

Before introducing a solved problem, we want to show Table 2-3 for relations between F&A&i,n.
To find A with given F F/A=(1+i)^n-1/(i), the standard notation F=A/F*(i%,n).

For the Excel sheet, the function is FV, or the future value function, used as F=FV*(i%,n, A).
The sinking fund is the value of A/F =i/((1+i)^n-1)).
For the symbolic expression, A =F*(A/F,i%,n), using an Excel sheet the function is PMT, or the future value function, used as F=PMT*(i%,n,F).
We can develop a relationship between P and A, since F= (A/i)*((1+i)^n-1)), F=P*(1+i)^n. A value of A can be obtained, A=(i*P)*(1+i)^n/((1+i)^n-1)).
To get if P is known, A=P*(A/P,i%,n). While P=A*(P/A,i%,n).
This is the pdf file used in the illustration of this post.
The next post title will be Uniform Series of Compound interest-2/2 in the Economy.
For a useful external resource, Engineering Economy. Applying Theory to Practice.

