False position method.
The false position method is another numerical method for root finding, The same Solved problem, will be used to get the root for f(x), but this time using another method that is called false position, or regula -falsi, which can be done by substituting the formula shown here.
Xr is the horizontal distance to the root point, where x1 and x2 are the distance from the point(0.0) to the first left bracket point and right bracket point, respectively.
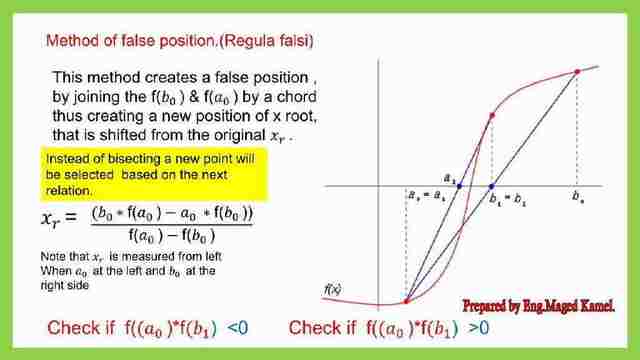
While b1 and b2, represent the value of the function at the left bracket point and the value of the function at the right bracket point.
A Solved problem for the false position method.
We have used previously the function for which f(x)=x^3 -6x^2 +11x-6. Find the zeros of the function by the False position method considering a0 as equal to 2.50 and b= 4. as before. xr numerator is (x right*yleft-x left*y right), while the denominator =(yleft- y right).
The steps are as follows:
1-The solution we have before a0 as =2.50 will give us an f(a0) =-0.375, and we have b. =4 that is giving f(b)= f(4)=+6.0.
2- If we assume that this is a sketch of the graph. If we assume that this is a sketch of the graph. The graph intersects the x-axis at a certain point, and now we would like to know what will be the x1 value and, accordingly, the function f(x1).
3- We apply in the equation of xr=((b0)*f(a0)- a0*f(b0))/(f(a0)-f(b0) The b0=4.0. and a0=2.50.
4-The function of f(b0) is 6, and the function of (a0)= f(a0)=-0.375 hen xr=((4-*0.375)-(2.50*6)/(-0.375-6) =2.588.
5- Our next step is trying to find what is the function, value at x1=2.588. So we plug in the function. by putting f(x)= f(2.588).We substitute the result as -0.3847.
This point is considered a new left bracket point.
6-We can make a left bracket here, and we have the bracket for the positive value again, the function of x at x=4 or b=4; it is a right bracket point.
We join this point with the other point that has a positive value. of +6.
Our false position again moves from a=2.50 to x =2.588. which is very close to the required x value that gives zero.

7- We apply in the equation of xr=((b0)*f(a0)- a0*f(b0))/(f(a0)-f(b0) The b0=4.0. and a0=2.588. f(a0)=-0.36801, b0=4, f(b0)=+6.
Our new value of xr=(4*(-0.38469)-(2.588)*(6))/(-0.38469-6)=2.673.
8- We will substitute in the function; we get f(2.673), which=-0.36801, and it will give (-)minus, which means it is the new left bracket. We can check f(2.673)f(4) is with a negative sign, that is, (-0.384696=-2.2085.
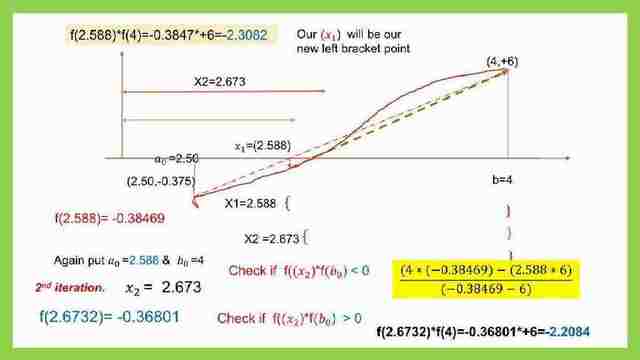
9- We apply in the equation of xr=((b0)*f(a0)- a0*f(b0))/(f(a0)-f(b0) The b0=4.0. and a0=2.673. f(a0)=-0.368019,b0=4, f(b0)=+6. Our new value of xr=(4*(-0.368019)-(2.588)*(6))/(-0.36801-6)=2.7499.
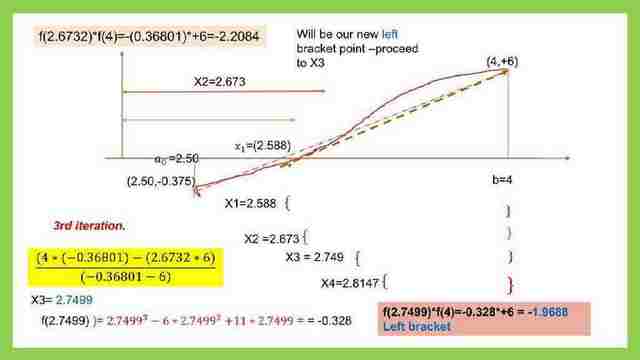
10-We will substitute in the function; we get f(2.749), which=-0.328, will give (-)minus, which means it is the new left bracket. We can check f(2.749)*f(4) is with a negative sign, that is, (-0.328*6)=-1.9688.
11- We apply in the equation of xr=((b0)*f(a0)- a0*f(b0))/(f(a0)-f(b0) The b0=4.0. and a0=2.7499. f(a0)=-0.328, b0=4, f(b0)=+6.
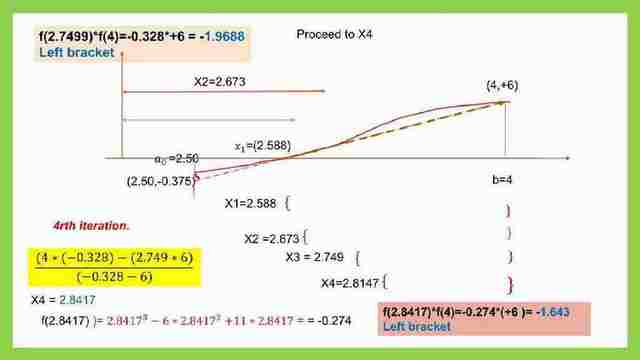
Our new value of xr=(4*(-0.328)-(2.7499)*(6))/(-0.328-6)=2.8147.- We apply in the equation of xr=((b0)*f(a0)- a0*f(b0))/(f(a0)-f(b0) The b0=4.0. and a0=2.673. f(a0)=-0.368019,b0=4, f(b0)=+6. Our new value of xr=(4*(-0.368019)-(2.588)*(6))/(-0.36801-6)=2.7499.
We will substitute in the function; we get f(2.8147), which=-0.2741, it will give (-)minus, which means it is the new left bracket. We can check f(2.8147)*f(4) is with a negative sign, that is, (-0.2741*6=-1.643.
We have reached x5, as we can see in the next slides, x5=2.866, with a -ve value, and again it is the new left bracket, coming closer to b=4. The details of the calculation are shown in the next image.
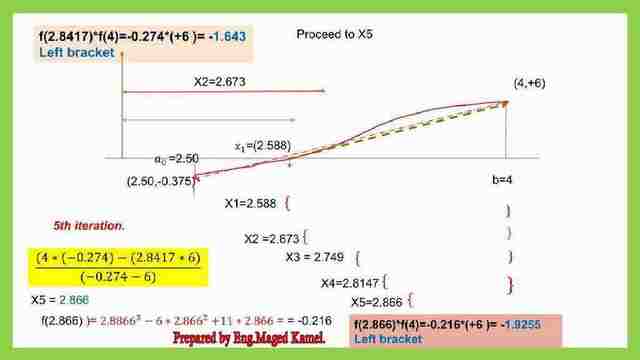
We plug in x=2.866 as a0. While f(2.866)=f(a0)=-0.216, we can get a new point of x=2.905. THIS POINT is a left bracket point.
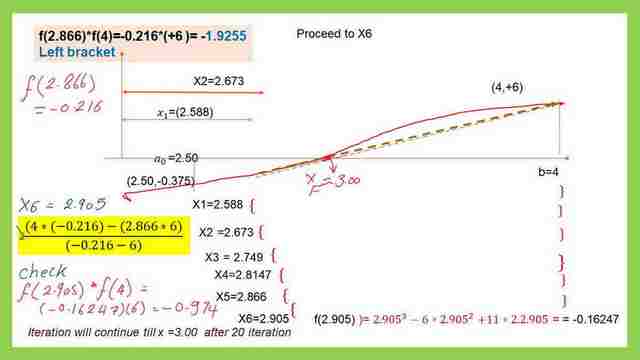
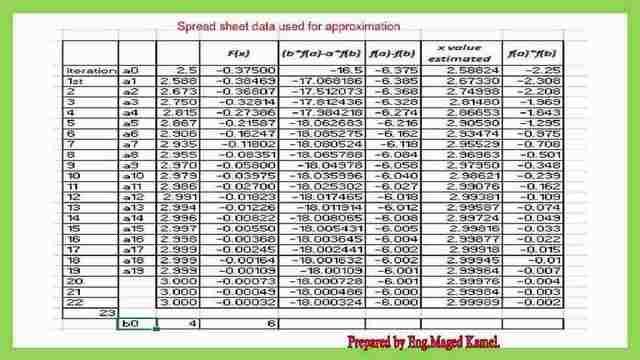
The table for the number of iterations.
This is the table for 20iterations at x20, the value =3.00. f(x=3)=0, the calculations are performed using an Excel sheet as shown in the next slide image.
The next post will be Fixed-point iteration and how to use it.
A very intersection source is Holistic Numerical methods.
