An easy approach to Compact and non-compact sections.
What is a compact section?
A compact section is one that can develop a plastic hinge before local buckling of the flange or the web, provided that adequate lateral bracing is provided.
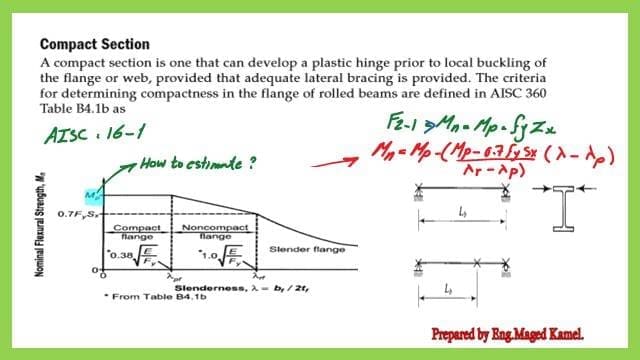
The table expresses the relation between lambda and MN, in three zones, as shown in the graph, the first zone is compact, while the second zone is non-compact, and the last zone is a slender flange.
If we draw the graph that represents the relation between the lambda λ and Plastic moment MP, considering λf=(bf/2tf) for flange, while for web λw=hw/tw. We start with the case of a flange, which is more critical since the lambda λ value for the web is nearly safe for most of the steel sections.
The vertical axis represents the nominal moment Mn. The design is based on what is called Plastic moment MP. The start of the graph is in the form of a straight line, from λ=0, till λ=λp.
In the case of the flange. The area under the straight line from λ=0, λp, is called a compact flange.
This can be achieved by placing concrete over the flange of the steel section. Through studs. the flange is kept in place, braced, and the buckling length will be=0. In that case, the steel section will be considered a compact section.
The criteria for determining the compactness of rolled beams are defined in AISC 360 Table 4.1b, please refer to the second slide.
The table expresses the relation between lambda and MN, in three zones, as shown in the graph, the first zone is compact, the second zone is non-compact, and the last zone is a slender flange.

What are the different zones for flanges?
The first zone is compact, in the case of a flange, the flange is prevented from moving laterally by providing a stud and the covering slab has a range from λf=0 to λf=λp.
The second zone for the lambda of the flange, lambda is called λrf. At that time the flange starts to have a lateral buckling. The flange section is considered a non-compact flange.
The third zone represents a slender flange. The slender flange behaves similarly to a column that has a lateral buckling. The next expression for lambda value for the flange, where Fy is the yield strength and E is the modulus of elasticity.
While for the value of λf=λFr=1.0*sqrt(E/Fy).
The first category, laterally supported compact beam, is quite common. For a case of doubly -symmetric, Compact I beam or c-shaped section bent on the major axis, AISC F2.1 gives the nominal strength as Mn= MP, where MP=Fy*ZX and Zx is the plastic section modulus.
This is a part of table B4.1b, quoted from Aisc 360 spec. For item 10 for the case of flanges of rolled I- shaped section, C channel, and Tees. lambda =b/t where b is the width of the C- channel, while for I beam and T section, b is considered as half the total width.


The next slide shows the different values of λf which are equal to (bf/2tf) when λf=λp. The value equals 0.38*sqrt(E/Fy) and can be set equal to 64.7/Sqr(Fy) for any value of Fy, while E=29000ksi. While when λf=λr, its value equals to1.00*sqrt(E/Fy) and can be set equal to 170.30/sqrt(Fy).


The web has three zones but with different values for lambda, as shown in the next slide. For The yield stress Fy value of 50 ksi, the approximate values are shown.
This is the pdf file used for the illustration of this post.
This is a link for a good external reference for steel beams.-A Beginner’s Guide to Structural Engineering
This is the next post, 3-Introduction to Plastic Theory.

