Last Updated on March 21, 2024 by Maged kamel

Fixed point iteration.

The objective of our lecture is to understand the following points, what is the meaning of fixed-point iteration? What is the linear approximation newton method of root finding?  We get x₁, using fixed-point iteration, if we plug in x₁ again we get X ₂.

We substitute we get X ₃, so we will repeat the process until the result of X obtained is the same for successive steps.

If you wish to review the PDF data used in the illustration, please continue reading.

All these methods are accompanied by solved problems. If we start x_0, then we get an expression for X₁. We substitute our first choice of the value of x.

Normally we write the function as Y is an f(x), but if we want to get an expression for x. We can put x on the left-hand side and readjust our equation by getting an expression f(x)=0, to be arranged as follows.

We put X on the left-hand side so it will become in the expression = g(x). The new form will be x_i=g(x). We can get a value to x starting by X =a

Solved example-1 using fixed-point iteration.

Solve numerically the following equation X^3+5x=20. Give the answer to 3 decimal places.
Start with X₀ = 2. Sometimes in the example, the author gives us a starting point then we rearrange the equation to become as follows:

1-We choose to let X ^3 on the left-hand side, so we are sending 5x with a negative sign.

2- The equation will become x^3=20-5x, then for the X value, we take the third root of the equation. So X is the 3rd root of (20-5*x) we call it g(x).

How to get x₁ value by fixed-point iteration?

3- Our starting value of x we call it x₀=2, this is a value that he has given us and substituted in the equation, then we get a value of x₁=2.154, the calculation can be viewed from the next equation.

How to get x₂ value by fixed-point iteration?

For the next point, we call it x₂.
4-If we plug that value here we get X₂ then if we substitute the X 2 value will become the third root of (20 -10.77) =2.098.

How to get x₃ value by fixed-point iteration?

5- Again we put the value of 2.098 in the expression of g(x), x₃=we get, X₃ which is 2.119, and use the value of X₃. We substitute we get X₄ the value is 2.111.

We proceed the same with x₄, we plug it here. We get X₅ and X₆ and X₇ and X₈. After 7 iterations, the right-hand side is close to a value of 20 for x₇=2.113.

The table indicates the different values based on the fixed-point iteration.

These are two graphs the upper one shows the f(x) function and its intersection with the x-axis. The root is between 2.1 and 2.11 for the function X^3+5x=20.

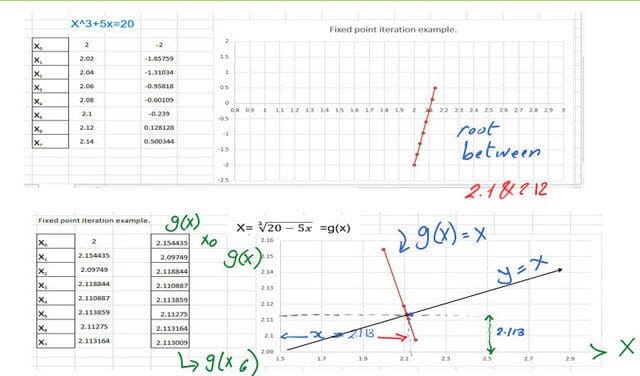
Using the fixed point iteration created a new function which is called g(x), the graph is shown. The intersection of g(x) with the function y=x, will give the root value, which is x₇=2.113

Solved example-2 using fixed-point iteration.

The solved example-2. It is required to find the root for x^4-x-10=0, the same procedure that we have adopted for the previous example will be followed. Create a g(x)=(10+x)^4, the initial point given is x₀=4. Plug in to get the value of x₁.

The slide image shows the table of points of x from x=4 till x=1.8555 and the corresponding value of g(x). We are looking for the intersection point between this g(x) and y=x, or simply when we plug in a certain value of x we get the same value in y. The point coordinate is (1.85555,1.8555), which is obtained from 6 iterations.

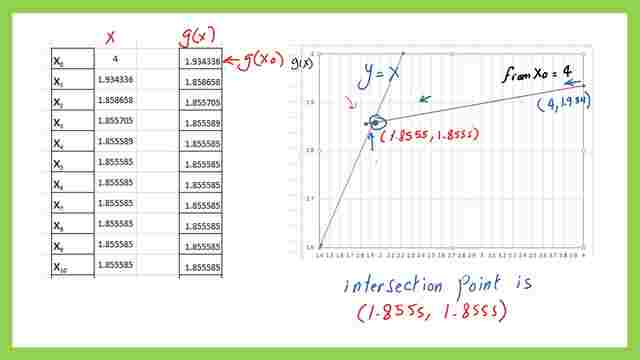
The curve is drawn with the shown x and Y-axis. The zero point will be very close to 1.8555. The slide image shows the table of points of x from x=4 till x=0.50 and the corresponding value of f(x).

We are looking for the intersection point between 1.75, and 2.00. The previous value of 1.8555, obtained from the fixed point iteration will give a y value close to 0.

This is a link to download the PDF used for the illustration of this post

The next post is the What is the Linear Approximation method?