Last Updated on March 11, 2026 by Maged kamel
Solved problem 4-13 to estimate stiffness reduction τb.
The content of post 26.
We will discuss solved problem 4-13 from Prof. Segui’s book.
In the next slide image, there are two equations as indicated in the AISC clause 16.1.27. There are two conditions. αPr/Pns <=0.50 and αPr/Pns>0.50.
Pr is the required axial compressive strength, either obtained by using LRFD or ASD. α =1 (LRFD) or α =1.6 (ASD). The Pns is the cross-sectional compressive strength=Ag*Fy for non-slender elements.
Let us review first. A test will be done to check that αPr/Pns < 0.50. There is no reduction; the same points will coincide with each other. Then τb = 1, but αPr/Pns > 0.50; in this case, the equation can be used.
Two values for α, for LRFD=1, while for the ASD, α=1.60.
Problem 4-13: A W10 x 54 of ASTM A992 is subjected to a service load of 100 kips and a service Live load of 200 kips. If the slenderness ratio makes this member an inelastic column, what is the stiffness reduction, τb? This means that kl/r is <4.71*sqrt(E/fy) for that column, which =113 for Fy= 50 ksi.
The stiffness reduction τb is to be estimated. For section W10x64, in our solved problem 4-13. We can get the gross area Ag, which is 15.80 inch2, after reviewing the data from the W section tables.
What information do we have? We cannot estimate τb in LRFD without evaluating Pult, the ultimate column load.
Check the value of α based on the data given.
If we start with the LRFD calculations, the value of Pult = 1.2D + 1.60L should be greater than 1.4D. We have DL = 100 kips and LL = 200 kips. Pult = 1.20*100 + 1.60*200, so Pult = 440 kips. For LRFD, α = 1; for ASD, α = 1.6.
First check that *αPr/Pns <=0.50, we have α=1, Pr=Pult=440 kips, Ag=15.80 inch2, Pns=Fy*Ag. Fy=50.0 ksi while Ag=15.80 inch2. Pns=50*15.80, then αPr/Pns=0.566, check this value with if >0.50 then τb<1, which in our case, since we have 0.556 >0.50, then τb <1.0.
How to use Table 4-13 for LRFD design?
The equation will be τb= 4(α*Pr/Pns)*(1-(α*Pr/Pns)).This term (αPr/Pns) exists outside and inside the bracket. Recall Pr=Pult=440 kips. The Pns=Py=50*15.80=790 kips with α=1, then τb=4((1440/790)*(1-(440/790))=0.987. If we wish to use the table, we will need Fult = Pult/AG. Fult=440/15.80. We need the stress value, which is 440/15.80 = 27.85 ksi.
The table is Table 4-13, and its title is “Stiffness Reduction Factor.” We have Fult = 27.85 ksi. This figure falls between 27 and 28 ksi. Using the table, we move horizontally from left to right at 27.0 ksi, which yields τb = 0.994.
Meanwhile, at Fcr = 28.0 ksi, we have τb = 0.986.
We perform interpolation, and then τb = 0.9872, which is close to the figure obtained from the general equation.
How to estimate τb for ASD Design.
Let us proceed with the ASD in our solved problem, 4-13. We will evaluate Pt=PD+PL=100+200=300 kips. The ultimate load, Py=Fy*Ag=50*15.80=790 kips.
Perform the first check, which we usually start with, considering α = 1.60. If αPr/Pns> 0.50, then we have α = 1.60, Pt = 330 kips. Perform the first check, which we usually start with, considering α = 1.60. If αPr/Pns > 0.50, then we have α = 1.60 and Pt = 330 kips.
Pns=790, then αPr/Pns=1.60*300/790=0.607>0.50, then τb will be < 1.0, and we perform our estimation from the equation. τb= 4(α*Pr/Pns)*(1-(αPr/Pns)), Pr=Pt=300 kips, Pns=790 kips, α=1.60. We apply this equation, and then τb = 0.9536.
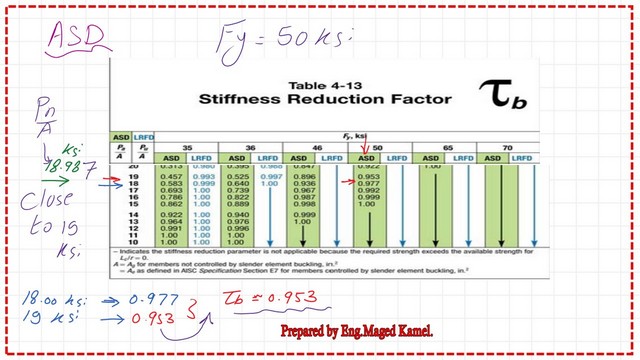
To use the table again, we need to have Ft = Pt/Ag, where Pt/Ag = 300 kips/15.80 ft = 18.989 ksi. We have Pe/A=18.98 KSI.
For Fy = 50 ksi. We draw a vertical line from Fy = 50 ksi at the ASD section, between 18 ksi and 19 ksi on the left side. We draw another line at the intersection. τb will be between 0.953 and 0.977 and can be estimated at 0.953.
Quick estimate for τb using formulas.
As a quick estimate of τb for the LRFD design, with Fcr = 27.848 ksi and Fy = 50 ksi, we obtain λ^2 = 1.772.
We proceed to estimate Fcr elastic from the equation of Fcr =Fy/λ^2=50/1.772=28.22 ksi. Divide Fc in/Fcr elastic to get the τb=27.85/28.22=0.987.
For the ASD design, we have Fcr = 19.0 ksi; we will multiply by alpha, α, which is 1.60.
For ASD design, Fcr = 1.6*19 = 30.40 ksi; Fy = 50 ksi. We get the λ^2 value as 1.568. We proceed to estimate Fcr elastic from the equation of Fcr =Fy/λ^2=50/1.568=31.89 ksi. Divide Fc in/Fcr elastic to get the τb=30.4/31.89=0.953.
The PDF file used to illustrate this post is available for viewing or download below.
This is the link to the previous post, “Stress Reduction Factor for Inelastic Columns.”
This is the next post, which is the solved problem, 4-14.
For a good A Beginner’s Guide to the Steel Construction Manual, 14th ed. Chapter 7 – Concentrically Loaded Compression Members.
For a good A Beginner’s Guide to the Steel Construction Manual, 15th ed. Chapter 7 – Concentrically Loaded Compression Members.
For a good A Beginner’s Guide to the Steel Construction Manual, 16th ed. Chapter 7 – Concentrically Loaded Compression Members.